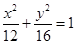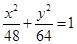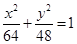题目内容
已知圆锥曲线 的离心率e为方程
的离心率e为方程 的两根,则满足条件的圆锥曲线的条数为 ( )
的两根,则满足条件的圆锥曲线的条数为 ( )
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:因为方程 的两根为
的两根为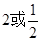 。①当e=2时,很显然圆锥曲线为双曲线,又由
。①当e=2时,很显然圆锥曲线为双曲线,又由 得
得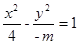 ,所以
,所以 ,因为
,因为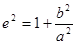 ,所以m=-12。此时满足条件的为一条。②当e=
,所以m=-12。此时满足条件的为一条。②当e=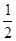 时,很显然圆锥曲线为椭圆,又由
时,很显然圆锥曲线为椭圆,又由 得
得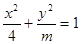 ,若焦点在x轴上,则
,若焦点在x轴上,则 ,因为
,因为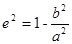 ,所以m=2。此时满足条件的为一条。若焦点在y轴上,则
,所以m=2。此时满足条件的为一条。若焦点在y轴上,则 ,因为
,因为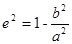 ,所以m=8。此时满足条件的为一条。因此共三条。
,所以m=8。此时满足条件的为一条。因此共三条。
考点:本题考查椭圆的标准方程及简单性质;双曲线的标准方程及简单性质。
点评:圆锥曲线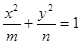 可能表示圆的方程、椭圆的方程、双曲线的方程。当
可能表示圆的方程、椭圆的方程、双曲线的方程。当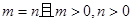 时,表示圆的方程;当
时,表示圆的方程;当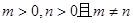 时,表示椭圆的方程;
时,表示椭圆的方程;
当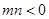 时,表示双曲线的方程。
时,表示双曲线的方程。

练习册系列答案
相关题目
已知椭圆 的长轴长为10,离心率
的长轴长为10,离心率 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. 或 或 | B. 或 或 |
C. 或 或 | D. 或 或 |
双曲线 上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
| A.1或13 | B.15 | C.13 | D.1 |
设直线 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 与椭圆
与椭圆 的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为
的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为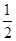 的点M的个数为
的点M的个数为
| A.1 | B.2 | C.3 | D.4 |
 上一点
上一点 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线 的左顶点为
的左顶点为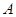 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线 平行,则实数
平行,则实数 的值是( )
的值是( )



 和双曲线
和双曲线 的公共焦点为
的公共焦点为 、
、  ,
, 是两曲线的一个交点,那么
是两曲线的一个交点,那么 的值是 ( )
的值是 ( )



 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: .给出下列三个命题:
.给出下列三个命题: ;
; 中,若∠C=90°,则
中,若∠C=90°,则 ;
; .
. 的两个焦点,过F2的直线交椭圆于点A、B,若
的两个焦点,过F2的直线交椭圆于点A、B,若 ,
,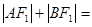 ( )
( ) 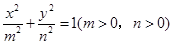 的右焦点与抛物线
的右焦点与抛物线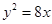 的焦点相同,离心率为
的焦点相同,离心率为 ,则此椭圆的方程为( )
,则此椭圆的方程为( )