题目内容
已知椭圆
的长轴长为10，离心率
，则椭圆的方程是（ ）
A． 或 | B． 或 |
C． 或 | D． 或 |
A
解析试题分析：因为由题意可知椭圆的长轴长为10，离心率，可知2a=10,a=5,同时
，那么结合
,由于焦点位置不确定，因此可知其方程有两种情况，故可知为或，进而选A.
考点：本题主要考查椭圆的简单性质．在没有注明焦点的位置时，一定要分长轴在x轴和y轴两种情况．
点评：解决该试题的关键是先根据题意求得a，进而根据离心率求得c，则根据a，b和c的关系求得b，则椭圆的方程可得.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
抛物线
的准线方程是（ ）
A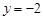． | B． | C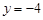． | D． |
经过点P（4，-2）的抛物线标准方程为（ ）
| A．y2=x或x2=-8y | B．y2=x或y2=8x |
| C．y2=-8x | D．x2=-8y |
若直线
和⊙O:
没有交点,则过
的直线与椭圆
的交点个数 ( )
| A．至多一个 | B．0个 | C．1个 | D．2个 |
已知圆锥曲线
的离心率e为方程
的两根，则满足条件的圆锥曲线的条数为 ( )
| A．1 | B．2 | C．3 | D．4 |
已知椭圆
和双曲线
,有相同的焦点,则椭圆与双曲线的离心率的平方和为（ ）
A． | B． | C．2 | D．3 |
若点
和点
分别为双曲线
（
）的中心和左焦点，点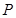
为双曲线右支上的任意一点，则
的取值范围为（ ）
A．[3-  ，  ） | B．[3+ ， ） |
C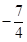．[ ， ） | D．[ ， ） |
抛物线
的焦点到准线的距离是（ ）
A． | B． | C． | D． |
抛物线
（p＞0）上一点M到焦点的距离是a，则M到y轴的距离是（ ）
| A．a-p | B． a+p | C．a-  | D．a+2p |