题目内容
椭圆
和双曲线
的公共焦点为
、 
,
是两曲线的一个交点，那么
的值是 （ ）
A． | B． | C． | D． |
A
解析试题分析：不妨设点在第一象限，因为在椭圆上，所以
,因为在双曲线上，所以
，两式联立，得
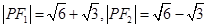，又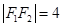
,根据余弦定理可以求得的值是.
考点：本小题主要考查圆锥曲线定义的应用和余弦定理的应用，考查学生运用所学知识解决问题的能力和转化能力及运算求解能力.
点评：圆锥曲线的定义在解题时经常用到，要加以重视.
练习册系列答案
阅读快车系列答案
相关题目
椭圆
的一条弦被
平分,那么这条弦所在的直线方程是 （ ）
A． | B． |
C． | D． |
已知双曲线x2－
＝1的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则
·
的最小值为( )
| A．－2 | B．－ | C．1 | D．0 |
的两焦点为
、
，以
为边作正三角形，若椭圆恰好平分该正三角形的另两边，则椭圆的离心率是（ ）
的中心在原点,焦点在
轴上,
的准线交于
两点,
;则
经过点P（4，-2）的抛物线标准方程为（ ）
| A．y2=x或x2=-8y | B．y2=x或y2=8x |
| C．y2=-8x | D．x2=-8y |
曲线y＝1＋
与直线y＝k(x－2)＋4有两个交点，则实数k的取值范围是( )
A．(0， ) | B．(，＋∞) |
C．( ， ] | D．(，] |
已知圆锥曲线
的离心率e为方程
的两根，则满足条件的圆锥曲线的条数为 ( )
| A．1 | B．2 | C．3 | D．4 |
、
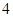
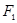分别是双曲线
的左右焦点，以坐标原点
为
为半径的圆与双曲线在第一象限的交点为
，则当
的面积等于
时，双曲线的离心率为（ ）
