题目内容
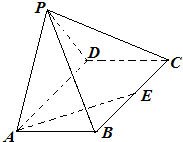
如图,面PAD⊥面ABCD,PA=PD,四边形ABCD是平行四边形,E是BC中点,AE=3,则
•
=______.
| CP |
| EA |

取AD得中点F,连接CF,由面PAD⊥面ABCD,PA=PD,四边形ABCD是平行四边形,E是BC中点,AE=3,
可得CFAE为平行四边形,PF垂直平面ABCD,故
•
=0,且
=
.
∴
•
=(
+
)•
=
•
+
•
=
2+0=9,
故答案为 9.
可得CFAE为平行四边形,PF垂直平面ABCD,故
| FP |
| EA |
| CF |
| EA |
∴
| CP |
| EA |
| CF |
| FP |
| EA |
| CF |
| EA |
| FP |
| EA |
| EA |
故答案为 9.

练习册系列答案
相关题目
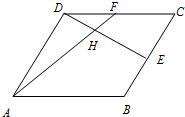
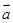 、
、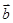 是非零向量,它们之间有如下一种运算:
是非零向量,它们之间有如下一种运算: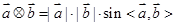 ,其中
,其中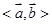 表示
表示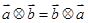 ;
;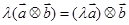 ;
;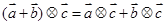 ;
;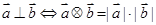 ;
;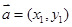 ,
,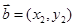 ,则
,则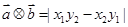 .
.