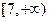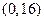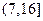题目内容
设向量
，
均为单位向量，且|
+
|=1，则
与
夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A．
| B．
| C．
| D．
|
设
与
的夹角为θ，
∵|
+
|=1，∴（
+
）2=
2+2
•
+
2=1…（*）
∵向量
、
均为单位向量，可得|
|=|
|=1
∴代入（*）式，得1+2
•
+1=1=1，所以
•
=-
根据向量数量积的定义，得|
|•|
|cosθ=-
∴cosθ=-
，结合θ∈[0，π]，得θ=
故选C
| a |
| b |
∵|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
∵向量
| a |
| b |
| a |
| b |
∴代入（*）式，得1+2
| a |
| b |
| a |
| b |
| 1 |
| 2 |
根据向量数量积的定义，得|
| a |
| b |
| 1 |
| 2 |
∴cosθ=-
| 1 |
| 2 |
| 2π |
| 3 |
故选C
练习册系列答案
芒果教辅达标测试卷系列答案
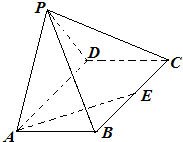
相关题目
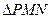中，
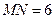，则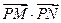
的取值范围是（ ）
