题目内容
【题目】符号![]() 表示不大于x的最大整数
表示不大于x的最大整数![]() ,例如:
,例如:![]() .
.
(1)解下列两个方程![]() ;
;
(2)设方程: ![]() 的解集为A,集合
的解集为A,集合![]() ,
,![]() ,求实数k的取值范围;
,求实数k的取值范围;
(3)求方程![]() 的实数解.
的实数解.
【答案】(1)![]() ,
,![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)根据对符号![]() 的定义理解可得答案;
的定义理解可得答案;
(2)将![]() 化为
化为![]() ,再分三种情况去绝对值解不等式可得集合
,再分三种情况去绝对值解不等式可得集合![]() ,然后对
,然后对![]() 分类讨论解得集合
分类讨论解得集合![]() ,再根据
,再根据![]() ,列式可求得
,列式可求得![]() 的范围;
的范围;
(3)先判断出![]() ,再将
,再将![]() 平方得
平方得![]() ,再结合方程
,再结合方程![]() 可得不等式
可得不等式![]() ,解不等式可得
,解不等式可得![]() 或
或![]() 或
或![]() 或
或![]() ,分别代入方程
,分别代入方程![]() 可解得答案.
可解得答案.
(1) ![]()
![]() ,
,
(2) ![]() ,
,![]() ,
,
当![]() 时,有
时,有![]() ,解得
,解得 ![]() ,
,
当![]() 时,有
时,有![]() ,
,![]() 无解,
无解,
当![]() 时,有
时,有![]() ,解得:
,解得: ![]()
综上所述:![]() .
.
因为![]()
当![]() 时,
时,![]()
因为![]() ,所以
,所以![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,解得:
,解得: ![]() ,
,
当![]() 时,
时,![]() ,
,![]() 成立,
成立,
综上: 实数k的取值范围![]() .
.
(3)因![]() , 又
, 又![]() 时,方程
时,方程![]() 不成立,
不成立,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
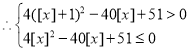 ,
,
所以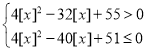
所以![]() ,
,
所以![]() 或
或![]() 且
且![]() ,
,
所以![]() 或
或![]() ,
,
所以![]() 或
或![]() 或
或![]() 或
或![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,所以
,所以![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,所以
,所以![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,
,
经检验知,这四个值都是原方程的解.
故方程![]() 的实数解为:
的实数解为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目