题目内容
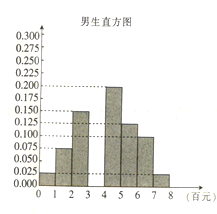
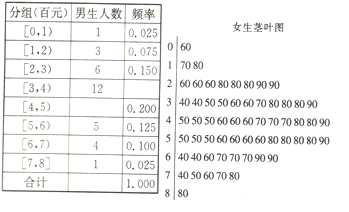
【题目】疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品,现随机抽取100件口罩进行检测,其结果如下:

(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据表中数据确定不合格的口罩数,再利用频数除以总数估计不合格率;
(2)根据平均数计算公式直接求解;
(3)先根据分层抽样确定抽取的5件口罩中不合格的1件,合格的4件,再利用枚举法列出基本事件总数以及至少有一件不合格品包含的基本事件数,最后根据古典概型概率公式以及对立事件概率公式求解.
解:(1)在抽取的100件产品中,不合格的口罩有:4+16=20(件)
所以口罩为不合格品的频率为![]() ,
,
根据频率可估计该公司所生产口罩的不合格率为![]() .
.
(2)平均测试分数为
![]() ·
·
(3)由题意所抽取的5件口罩中不合格的1件,合格的4件.
设4件合格口罩记为a,b,c,d,1件不合格口罩记为x.
若抽取的口罩中恰有1件不合格,则共有ax,bx,cx,dx,4种情况.·
而从5件口罩中抽取2件,共有ab,ac,ad,ax,bc,bd,bx,cd,cx,dx,![]() 种情况.
种情况.
所以2件口罩中至少有一件不合格品的概率为![]() .
.
故2件口罩全是合格品的概率为![]() .
.

【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 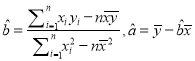 .
.