题目内容
【题目】已知函数f（x）＝lg（3＋x）＋lg（3－x）．
（1）判断
的奇偶性并加以证明；
（2）判断的单调性（不需要证明）；
（3）解关于m的不等式f（ m ）- f（ m+1）﹤0．
【答案】（1）偶函数，证明见解析；（2）
在
上是增函数，在
上是减函数；（3）
．
【解析】
试题(1)由
解析式，可先确定函数定义域，再运用奇偶性定义进行证明.
（2）有题可先对函数进行化简：
再设出中间量;
,运用复合函数的单调性进行分析，即：
增大，
增大，
也增大，为增区间.反之为减区间.
（3）结合（1）和（2）中的函数性质．可化为比较函数的自变量，列出不等组（需考虑定义域，求解．
试题解析：（1）由
，得－3＜x＜3，∴ 函数f(x)的定义域为(－3，3)．
函数f(x)的定义域关于原点对称，且f(－x)＝lg(3－x)＋lg(3＋x)＝f(x)，
∴ 函数f(x)为偶函数．
（2）、
,
为增函数
在（-3,0）上是增函数，在（0,3）上是减函数，
∴ f(x)在（-3,0）上是增函数，在（0,3）上是减函数
（3）
，
由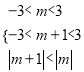
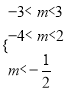
练习册系列答案
快捷英语周周练系列答案
相关题目
