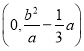题目内容
【题目】已知椭圆![]() 的左右焦点分别为F1,F2,该椭圆与y轴正半轴交于点M,且△MF1F2是边长为2的等边三角形.
的左右焦点分别为F1,F2,该椭圆与y轴正半轴交于点M,且△MF1F2是边长为2的等边三角形.
(1)求椭圆的标准方程;
(2)过点F2任作一直线交椭圆于A,B两点,平面上有一动点P,设直线PA,PF2,PB的斜率分别为k1,k,k2,且满足k1+k2=2k,求动点P的轨迹方程.
【答案】(1)![]() ;(2)x=4.
;(2)x=4.
【解析】
(1)根据椭圆的定义可得![]() ,从而可求出椭圆的方程.
,从而可求出椭圆的方程.
(2)设过点F2的直线方程为y=![]() (x﹣1)(当斜率存在时),设A(x1,y1),B(x2,y2),P(x0,y0),将直线与椭圆方程联立,利用韦达定理求出两根之和、两根之积,用两点表示出直线的斜率,代入k1+k2=2k,化简即可求解;当直线斜率不存在时,验证是否满足求出的轨迹方程即可.
(x﹣1)(当斜率存在时),设A(x1,y1),B(x2,y2),P(x0,y0),将直线与椭圆方程联立,利用韦达定理求出两根之和、两根之积,用两点表示出直线的斜率,代入k1+k2=2k,化简即可求解;当直线斜率不存在时,验证是否满足求出的轨迹方程即可.
(1)由题意可知:b=|OM|![]() ,a=|MF1|=2,
,a=|MF1|=2,
所以椭圆标准方程为![]() .
.
(2)①设过点F2的直线方程为y=![]() (x﹣1)(当斜率存在时),
(x﹣1)(当斜率存在时),
设A(x1,y1),B(x2,y2),P(x0,y0),
联立方程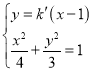 ,得到(3+4
,得到(3+4![]() 2)x2﹣8
2)x2﹣8![]() 2x+4
2x+4![]() 2﹣12=0,
2﹣12=0,
其中![]() ,
,![]() ,y1=
,y1=![]() (x1﹣1),y2=
(x1﹣1),y2=![]() (x2﹣1),
(x2﹣1),
由k1+k2=2k得:![]() ,
,
通分代入得:![]() ,
,
即(x0﹣4)(![]() (x0﹣1)﹣y0)=0,y0=
(x0﹣1)﹣y0)=0,y0=![]() (x0﹣1)舍去,所以x0=4,
(x0﹣1)舍去,所以x0=4,
②当直线斜率k不存在时,即为x=1,经验证可知直线x0=4上任意一点亦满足条件.
所以点P的轨迹的方程为x=4.

练习册系列答案
相关题目