题目内容
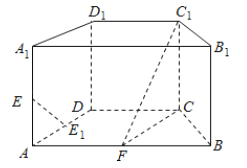
【题目】如图，四边形
为正方形，四边形
为矩形，且平面与平面互相垂直．若多面体
的体积为
，则该多面体外接球表面积的最小值为（ ）
A.
B.
C.
D.
【答案】A
【解析】
设正方形
的边长为a，矩形
的高为b，则长为
，由面面垂直的性质定理与线面垂直的判定定理可分别证得
平面与
平面，且由对称性以及棱锥的体积公式表示多面体
的体积，进而得到
，再由球体的表面积公式表示表面积，最后用基本不等式求得最值即可.
设正方形的边长为a，矩形的高为b，则长为，
因为正方形，则
，设
，又因为平面与平面互相垂直，
平面，平面
平面
，
所以平面，故
，
由题意可知，
，则
，即，
设矩形的对角线的交点为O，链接
，可得
，而
平面，且平面与平面互相垂直，平面平面，所以平面，可得
（R为外接球的半径），
所以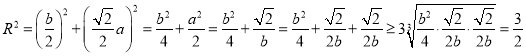
，当且仅当
时取等号，
故外接球的表面积为
故选：A
练习册系列答案
相关题目
