题目内容
【题目】某校组织甲、乙、丙、丁、戊、己等6名学生参加演讲比赛，采用抽签法决定演讲顺序，在“学生甲和乙都不是第一个出场，且甲不是最后一个出场”的前提下，学生丙第一个出场的概率为__________．
【答案】
【解析】
由条件概率计算方式，分别计算事件A：“学生甲和乙都不是第一个出场，且甲不是最后一个出场”的基本事件个数，其中分两类乙在最后与乙不在最后计数，与事件AB的基本事件个数，最后由公式求解即可.
设事件A：“学生甲和乙都不是第一个出场，且甲不是最后一个出场”；事件B：“学生丙第一个出场”，
对事件A，甲和乙都不是第一个出场，第一类：乙在最后，则优先从中间4个位置中选一
个给甲，再将余下的4个人全排列有
种；第二类：乙没有在最后，则优先从中间4
个位置中选两个给甲乙，再将余下的4个人全排列有
种，故总的有
.
对事件AB，此时丙第一个出场，优先从除了甲以外的4人中选一人安排在最后，再将余下的4人全排列有种
故
.
故答案为：
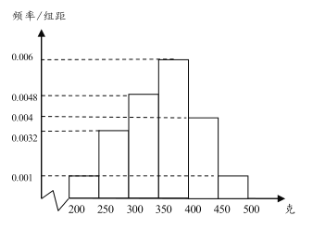
名校课堂系列答案
【题目】某机构对某市工薪阶层的收入情况与超前消费行为进行调查，随机抽查了200人，将他们的月收入（单位：百元）频数分布及超前消费的认同人数整理得到如下表格：
月收入（百元） |
|
|
|
|
|
|
频数 | 20 | 40 | 60 | 40 | 20 | 20 |
认同超前消费的人数 | 8 | 16 | 28 | 21 | 13 | 16 |
（1）根据以上统计数据填写下面
列联表，并回答是否有99%的把握认为当月收入以8000元为分界点时，该市的工薪阶层对“超前消费”的态度有差异；
月收入不低于8000元 | 月收入低于8000元 | 总计 | |
认同 | |||
不认同 | |||
总计 |
（2）若从月收入在
的被调查对象中随机选取2人进行调查，求至少有1个人不认同“超前消费”的概率.
参考公式：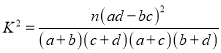
（其中
）.
附表：
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某地区某农产品近几年的产量统计如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根据表中数据，建立
关于的线性回归方程
；
（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据
，其回归直线的斜率和截距的最小二乘估计分别为：
，
.(参考数据:
，计算结果保留小数点后两位）