题目内容
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 分别是
分别是![]()
![]()
![]() 的中点.
的中点.
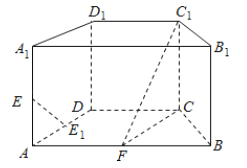
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与面
与面![]() 所成角的大小;
所成角的大小;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,证明
,证明![]() 为平行四边形,且
为平行四边形,且![]() ,再由三角形中位线证明
,再由三角形中位线证明![]() ,最后由线面平行的判定定理证明即可;
,最后由线面平行的判定定理证明即可;
(2)作![]() 交
交![]() 于点
于点![]() ,由线面垂直关系得到直线
,由线面垂直关系得到直线![]() 与面
与面![]() 所成角为
所成角为![]() ,再根据
,再根据![]() 是正三角形求解即可;
是正三角形求解即可;
(3)由(2)知,![]() 平面
平面![]() ,再证明
,再证明![]() 和
和![]() 分别垂直于
分别垂直于![]() ,求出直线
,求出直线![]() 与面
与面![]() 所成角为
所成角为![]() ,再求出
,再求出![]() 和
和![]() 的长度即可求解.
的长度即可求解.
(1)在直四棱柱![]() 中,取
中,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,![]() ,且
,且![]() ,所以
,所以![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又因为![]()
![]() 分别是棱
分别是棱![]()
![]() 的中点,
的中点,
所以![]() ,所以
,所以![]() ,
,
因为![]() .所以
.所以![]()
![]()
![]()
![]() 四点共面,
四点共面,
所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
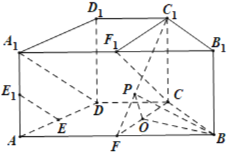
(2)因为![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点,
的中点,
所以![]() ,
,![]() 为正三角形,
为正三角形,
取![]() 的中点
的中点![]() ,则
,则![]() ,
,
又因为直四棱柱![]() 中,
中,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 平面
平面![]() ,即直线
,即直线![]() 与面
与面![]() 所成角为
所成角为![]() ,
,
所以![]() ,即
,即![]() ,
,
所以直线![]() 与面
与面![]() 所成角为
所成角为![]() .
.
(3)过![]() 在平面
在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
因为![]() 面
面![]() ,即
,即![]() ,
,
且![]() 与
与![]() 相交于点
相交于点![]() ,故
,故![]() 且
且![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在正三角形![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
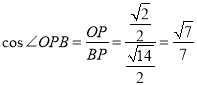 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某机构对某市工薪阶层的收入情况与超前消费行为进行调查,随机抽查了200人,将他们的月收入(单位:百元)频数分布及超前消费的认同人数整理得到如下表格:
月收入(百元) |
|
|
|
|
|
|
频数 | 20 | 40 | 60 | 40 | 20 | 20 |
认同超前消费的人数 | 8 | 16 | 28 | 21 | 13 | 16 |
(1)根据以上统计数据填写下面![]() 列联表,并回答是否有99%的把握认为当月收入以8000元为分界点时,该市的工薪阶层对“超前消费”的态度有差异;
列联表,并回答是否有99%的把握认为当月收入以8000元为分界点时,该市的工薪阶层对“超前消费”的态度有差异;
月收入不低于8000元 | 月收入低于8000元 | 总计 | |
认同 | |||
不认同 | |||
总计 |
(2)若从月收入在![]() 的被调查对象中随机选取2人进行调查,求至少有1个人不认同“超前消费”的概率.
的被调查对象中随机选取2人进行调查,求至少有1个人不认同“超前消费”的概率.
参考公式: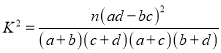 (其中
(其中![]() ).
).
附表:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |

