Question

【题目】F1 ， F2分别是双曲线x2﹣ =1（b＞0）的左、右焦点，过F2的直线l与双曲线的左右两支分别交于A，B两点，若△ABF1是等边三角形，则该双曲线的虚轴长为（ ）
A.2
B.2
C.
D.4

Answer 1

【答案】A
【解析】解：根据题意，如图△ABF1是等边三角形，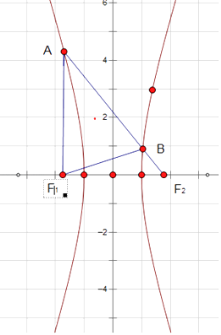

则有|AB|=|AF1|=|BF1|，
双曲线的方程为x2﹣ =1（b＞0），其中a=1，
A在双曲线上，则|AF2|﹣|AF1|=2a=2，
又由|AB|=|AF1|，即|BF2|=2，
B也在双曲线上，|BF1|﹣|BF2|=2a=2，
又由|BF2|=2，则|BF1|=2+2=4，
在△BF1F2中，|BF2|=2，|BF1|=4，∠F1BF2=120°，
则|F1F2|= =2 ，
即2c=2 ，
则c= ，
又由a=1，则b= = ，
则双曲线的虚轴长2b=2 ；
故选：A．