题目内容
【题目】已知椭圆C： 
+ 
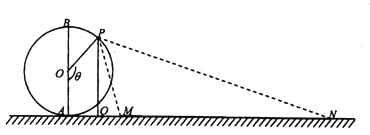
=1的左、右焦点分别为F1 ， F2 ， 直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直于直线l1于点P，线段PF2的垂直平分线与l1的交点的轨迹为曲线C2 ， 若点Q是C2上任意的一点，定点A（4，3），B（1，0），则|QA|+|QB|的最小值为（ ）
A.6
B.3 
C.4
D.5
【答案】D
【解析】解：∵圆C： 
+ 
=1的左右焦点为F1 ， F2 ，
∴F1（﹣1，0），F2（1，0），直线l1：x=﹣1，
设l2：y=t，设P（﹣1，t），（t∈R），M（x，y），
则y=t，且|MP|=|MF2|，
∴（x+1）2=（x﹣1）2+y2 ，
∴曲线C2：y2=4x，
则B（1，0）为曲线C2：y2=4x焦点，
过Q做QQ′垂直于曲线C2的准线，
由抛物线的定义可知：丨QQ′丨=丨QB丨，
|QA|+|QB|=|QA|+|QQ′丨，当A，Q，Q′三点共线时，|QA|+|QQ′丨取最小值，
则Q′（﹣1，3），则|QA|+|QQ′丨的最小值为4﹣（﹣1）=5，
∴|QA|+|QB|的最小值5，
故选D．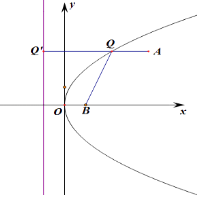
练习册系列答案
相关题目
