题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)设![]() ,若函数
,若函数![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
【答案】(1) 当![]() 时,增区间为
时,增区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)通过函数![]() ,得
,得![]() ,然后结合
,然后结合![]() 与0的关系对a的正负进行讨论即可;(2)对a的正负进行讨论:当a<0时,
与0的关系对a的正负进行讨论即可;(2)对a的正负进行讨论:当a<0时, ![]() 不可能恒成立;当a=0时,此时ab=0;当a>0时,由题结合(1)得
不可能恒成立;当a=0时,此时ab=0;当a>0时,由题结合(1)得![]() ,设
,设![]() ,问题转化为求
,问题转化为求![]() 的最大值,利用导函数即可.
的最大值,利用导函数即可.
试题解析::(1)由函数![]() ,可知
,可知![]() ,
,
![]() 时,
时, ![]() ,函数
,函数![]() 在R上单调递增;
在R上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
故当![]() 时,
时, ![]() ,此时
,此时![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增.
单调递增.
综上所述,当![]() 时,函数
时,函数![]() 在单调递增区间为
在单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
(2)由(1)知,当![]() 时,函数
时,函数![]() 在R上单调递增且当
在R上单调递增且当![]() 时,
时, ![]() 不可能恒成立;
不可能恒成立;
当a=0时,此时ab=0;
当a>0时,由函数![]() 对任意x∈R都成立,可得
对任意x∈R都成立,可得![]() ,
,
∵![]() ,
,
设![]() ,则
,则![]() ,
,
由于![]() ,令
,令![]() ,得
,得![]()
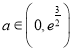 时,
时, ![]() 单调递增;
单调递增;
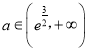 时,
时, ![]() 单调递减.
单调递减.
![]() ,即当
,即当![]() 时,ab的最大值为
时,ab的最大值为![]() .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目