题目内容
8．已知i为虚数单位，则 $\frac{1}{i}+{i^{2015}}$=（ ）| A． | 0 | B． | 2 | C． | 2i | D． | -2i |
分析 对 $\frac{1}{i}+{i^{2015}}$两部分分别化简，再求和．
解答 解：$\frac{1}{i}+{i^{2015}}$=-i+（i4）503i3=-i-i=-2i；
故选D．
点评 本题考查了虚数单位i的性质；熟记i2=-1是关键．
练习册系列答案
相关题目
19．已知数列{an}满足a1=2，an+1=$\frac{{1+{a_n}}}{{1-{a_n}}}$，则a15等于（ ）
| A． | 2 | B． | -3 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{3}$ |
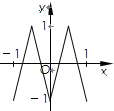
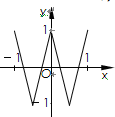
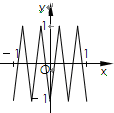
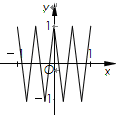
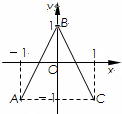如图，函数y=f（x）的图象为折线ABC，设g（x）=f[f（x）]，则函数y=g（x）的图象为（ ）
