Question

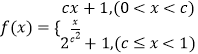【题目】已知函数 ，且 ．
（1）求实数c的值；
（2）解不等式 ．

Answer 1

【答案】
（1）解：∵0＜c＜1，

∴c2＜c，又f（c2）= ，即c3+1= ，

解得c= ；

（2）解：∵f（x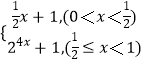）= ，由f（x）＞ +1得：

当0＜x＜ 时，解得 ＜x＜ ；

当 ≤x＜1时解得 ≤x＜1，

∴f（x）＞ +1的解集为{x| ＜x＜1}

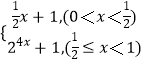【解析】（1）由题意知，0＜c＜1，于是c2＜c，从而由f（c2）= 即可求得实数c的值；（2）利用f（x）= ，解不等式f（x）＞ +1即可求得答案．
【考点精析】本题主要考查了函数的零点的相关知识点，需要掌握函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点才能正确解答此题．