题目内容
【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=![]() ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
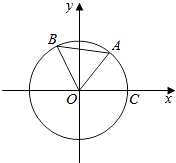
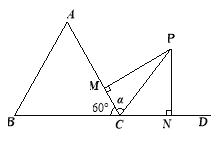
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


【答案】(1)![]() (2)α=
(2)α=![]() 时,PM+PN取得最大值2
时,PM+PN取得最大值2![]() .
.
【解析】
试题分析:(1)解三角形,就是利用正余弦定理将边角统一,本题求角,应利用正弦定理将边化为角:sinAcosA=sinBcosB,再根据二倍角公式及诱导公式求角:sin2A=sin2B, A=B或A+B=![]() .因为C=
.因为C=![]() ,所以A=B,A=
,所以A=B,A=![]() .(2)求PM+PN的最大值,首先建立函数关系式,取自变量为角:PM+PN=2sinα+2sin (α+
.(2)求PM+PN的最大值,首先建立函数关系式,取自变量为角:PM+PN=2sinα+2sin (α+![]() )=3sinα+
)=3sinα+![]() cosα=2
cosα=2![]() sin(α+
sin(α+![]() ).再根据基本三角函数求其最值:因为α∈(0,
).再根据基本三角函数求其最值:因为α∈(0,![]() ),所以α+
),所以α+![]() ∈(
∈(![]() ,
,![]() ),从而有sin(α+
),从而有sin(α+![]() )∈(
)∈(![]() ,1],因此当α+
,1],因此当α+![]() =
=![]() ,即α=
,即α=![]() 时,PM+PN取得最大值2
时,PM+PN取得最大值2![]() .
.
试题解析:(1)由acosA=bcosB及正弦定理可得sinAcosA=sinBcosB,
即sin2A=sin2B,又A∈(0,π),B∈(0,π),
所以有A=B或A+B=![]() . 2分
. 2分
![]() ,得A+B=
,得A+B=![]() ,与A+B=
,与A+B=![]() 矛盾,所以A=B,
矛盾,所以A=B,
因此A=![]() . 4分
. 4分
(2)由题设,得
在Rt△PMC中,PM=PC·sin∠PCM=2sinα;
在Rt△PNC中,PN=PC·sin∠PCN= PC·sin(π-∠PCB)
=2sin[π-(α+![]() )]=2sin (α+
)]=2sin (α+![]() ),α∈(0,
),α∈(0,![]() ). 6分
). 6分
所以,PM+PN=2sinα+2sin (α+![]() )=3sinα+
)=3sinα+![]() cosα=2
cosα=2![]() sin(α+
sin(α+![]() ). 10分
). 10分
因为α∈(0,![]() ),所以α+
),所以α+![]() ∈(
∈(![]() ,
,![]() ),从而有sin(α+
),从而有sin(α+![]() )∈(
)∈(![]() ,1],
,1],
即2![]() sin(α+
sin(α+![]() )∈(
)∈(![]() ,2
,2![]() ].
].
于是,当α+![]() =
=![]() ,即α=
,即α=![]() 时,PM+PN取得最大值2
时,PM+PN取得最大值2![]() . 14分
. 14分

 巧学巧练系列答案
巧学巧练系列答案