题目内容
6．计算：$\frac{{x}^{2}+3x+9}{{x}^{3}-27}$+$\frac{6x}{9x-{x}^{3}}$-$\frac{x-1}{6+2x}$．分析 利用立方差公式，平方差公式，及完全平方公式等化简$\frac{{x}^{2}+3x+9}{{x}^{3}-27}$+$\frac{6x}{9x-{x}^{3}}$-$\frac{x-1}{6+2x}$即可．
解答 解：$\frac{{x}^{2}+3x+9}{{x}^{3}-27}$+$\frac{6x}{9x-{x}^{3}}$-$\frac{x-1}{6+2x}$
=$\frac{{x}^{2}+3x+9}{（x-3）（{x}^{2}+3x+9）}$+$\frac{6}{（3-x）（3+x）}$-$\frac{1}{2}$•$\frac{x-1}{x+3}$
=$\frac{2（x+3）-12-（x-3）（x-1）}{2（x-3）（x+3）}$
=-$\frac{（x-3）^{2}}{2（x-3）（x+3）}$=$\frac{3-x}{2（x+3）}$．
点评 本题考查了分式的化简与公式的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
16．集合A={0，2}，B={1，a2}，若A∪B={0，1，2，4}，则实数a的值为（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | ±$\sqrt{2}$ |
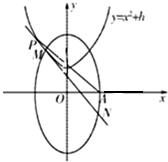已知焦点在y轴上的椭圆C1：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点Q（$\frac{\sqrt{3}}{2}$，1），过椭圆的一个焦点且垂直长轴的弦长为1．