题目内容
(本小题满分14分)已知函数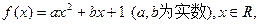
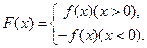
(1)若不等式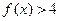 的解集为
的解集为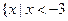 或
或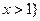 ,求
,求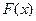 的表达式;
的表达式;
(2)在(1)的条件下, 当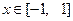 时,
时,  是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设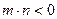 ,
, 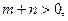
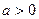 且
且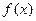 为偶函数, 判断
为偶函数, 判断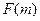 +
+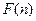 能否大于零?
能否大于零?
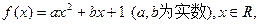
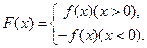
(1)若不等式
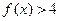 的解集为
的解集为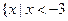 或
或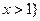 ,求
,求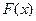 的表达式;
的表达式;(2)在(1)的条件下, 当
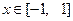 时,
时,  是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;(3)设
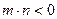 ,
, 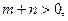
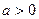 且
且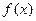 为偶函数, 判断
为偶函数, 判断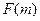 +
+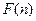 能否大于零?
能否大于零?(1)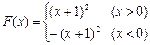
(2)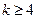 或
或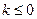
(3)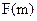 +
+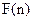 能大于零.
能大于零.
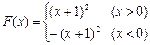
(2)
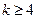 或
或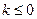
(3)
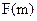 +
+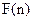 能大于零.
能大于零.(1)由已知不等式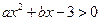 的解集为
的解集为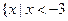 或
或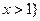 ,故
,故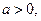 且方程
且方程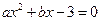 的两根为
的两根为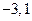 ,由韦达定理,得
,由韦达定理,得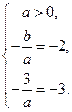 解得
解得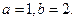 因此,
因此,
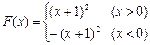
(2) 则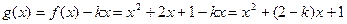
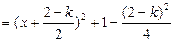 ,
,
当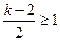 或
或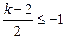 时, 即
时, 即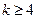 或
或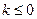 时,
时,  是单调函数.
是单调函数.
(3) ∵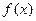 是偶函数∴
是偶函数∴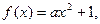
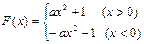 ,
,
∵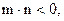 设
设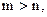 则
则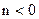 .又
.又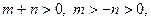 ∴
∴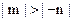
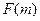 +
+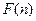
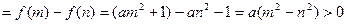 ,
,
∴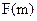 +
+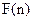 能大于零.
能大于零.
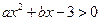 的解集为
的解集为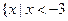 或
或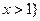 ,故
,故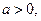 且方程
且方程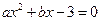 的两根为
的两根为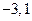 ,由韦达定理,得
,由韦达定理,得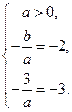 解得
解得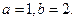 因此,
因此,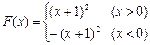
(2) 则
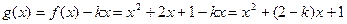
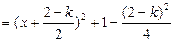 ,
, 当
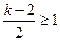 或
或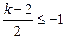 时, 即
时, 即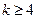 或
或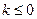 时,
时,  是单调函数.
是单调函数.(3) ∵
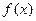 是偶函数∴
是偶函数∴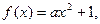
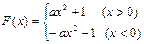 ,
, ∵
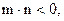 设
设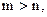 则
则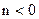 .又
.又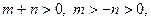 ∴
∴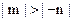
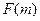 +
+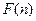
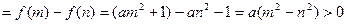 ,
,∴
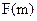 +
+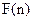 能大于零.
能大于零. 
练习册系列答案
相关题目
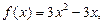
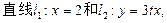
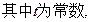
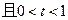 。直线l2与函数
。直线l2与函数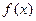 的图象以及直线l1、l2与函数
的图象以及直线l1、l2与函数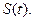
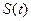 的解析式;
的解析式;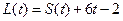 ,判断
,判断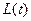 是否存在极值,若存在,求出极值,若不存在,说明理由;
是否存在极值,若存在,求出极值,若不存在,说明理由;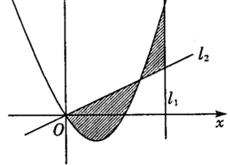
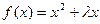 (x∈N*)是单调增函数,则实数
(x∈N*)是单调增函数,则实数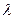 的取值范围是( )
的取值范围是( )



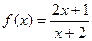 ,则
,则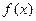 的对称中心是
的对称中心是 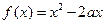 在区间
在区间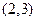 上有单调性,则实数
上有单调性,则实数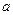 的范围是 ;
的范围是 ; 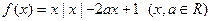 有下列四个结论:
有下列四个结论: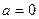 时,
时,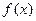 的图象关于原点对称
的图象关于原点对称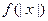 有最小值
有最小值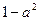
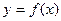 的图象与直线
的图象与直线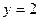 有两个不同交点,则
有两个不同交点,则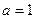
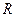 上是增函数,则
上是增函数,则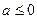

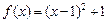 ,求
,求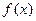 在区间
在区间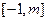 上的最小值
上的最小值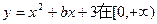 上是单调函数,则有 ( )
上是单调函数,则有 ( )



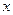 的方程
的方程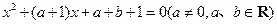 的两实根为
的两实根为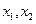 ,若
,若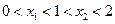 ,则
,则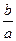 的取值范围是( )
的取值范围是( )


