题目内容
【题目】已知椭圆C:
（a＞b＞0）的两个焦点分别为F1（－
，0）、F2（，0）.点M（1，0）与椭圆短轴的两个端点的连线相互垂直.
（1）求椭圆C的方程；
（2）已知点N的坐标为（3，2），点P的坐标为（m，n）（m≠3）.过点M任作直线l与椭圆C相交于A、B两点，设直线AN、NP、BN的斜率分别为k1、k2、k3，若k1＋k3＝2k2，试求m，n满足的关系式.
【答案】（1）
；（2）m－n－1＝0
【解析】
试题（1）利用M与短轴端点构成等腰直角三角形，可求得b的值，进而得到椭圆方程；（2）设出过M的直线l的方程，将l与椭圆C联立，得到两交点坐标关系，然后将k1＋k3表示为直线l斜率的关系式，化简后得k1＋k3＝2，于是可得m，n的关系式.
试题解析：（1）由题意，c＝
，b＝1，所以a＝
故椭圆C的方程为
（2）①当直线l的斜率不存在时，方程为x＝1，代入椭圆得，y＝±
不妨设A（1，），B（1，－）
因为k1＋k3＝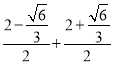
＝2
又k1＋k3＝2k2，所以k2＝1
所以m，n的关系式为
＝1，即m－n－1＝0
②当直线l的斜率存在时，设l的方程为y＝k（x－1）
将y＝k（x－1）代入，
整理得：（3k2＋1）x2－6k2x＋3k2－3＝0
设A（x1，y1），B（x2，y2），则
又y1＝k（x1－1），y2＝k（x2－1）
所以k1＋k3＝
＝
＝
＝
＝
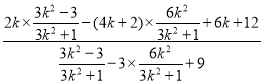
＝2
所以2k2＝2，所以k2＝＝1
所以m，n的关系式为m－n－1＝0
综上所述，m，n的关系式为m－n－1＝0.
【题目】某市调硏机构对该市工薪阶层对“楼市限购令”态度进行调查，抽调了50名市民，他们月收入频数分布表和对“楼市限购令”赞成人数如下表：
月收入（单位：百元） |
|
|
|
|
|
|
频数 | 5 |
| 10 | 5 | 5 | |
频率 | 0.1 |
|
| 0.2 | 0.1 | 0.1 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
（1）若所抽调的50名市民中，收入在
的有15名，求
，
，
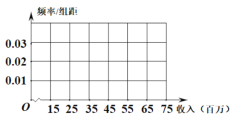
的值，并完成频率分布直方图．
（2）若从收入（单位：百元）在
的被调查者中随机选取2人进行追踪调查，选中的2人中恰有
人赞成“楼市限购令”，求的分布列与数学期望．
（3）从月收入频率分布表的6组市民中分别随机抽取3名市民，恰有一组的3名市民都不赞成“楼市限购令”，根据表格数据，判断这3名市民来自哪组的可能性最大？请直接写出你的判断结果．
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气
数值的影响，进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
与空气数值不合格的天数
进行统计分析，得出下表数据：
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
（1）以统计数据为依据，求出关于的线性回归方程
；
（2）根据（1）求出的线性回归方程，预测该市烧煤取暖的天数为20时空气数值不合格的天数．
参考公式：
，
．