题目内容
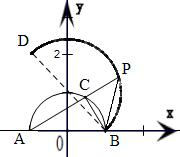
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )

| A.2π | B.
| C.π | D.4
|

连结BP,根据题意可得△BCP是以C为直角顶点的等腰直角三角形.
∴∠APB=45°,即直线PA到PB的角为45°,
设P(x,y),可得kPA=
,kPB=
,
∴tan45°=
=1,
化简得x2+(y-1)2=2.
∴点P的轨迹方程为x2+(y-1)2=2,
由已知y≥0可得kPA=
>0,
可知P点的轨迹是以(0,1)为圆心、半径r=
的半圆,
可得轨迹的长度是
×2πr=
π.
故选:B
∴∠APB=45°,即直线PA到PB的角为45°,
设P(x,y),可得kPA=
| y |
| x+1 |
| y |
| x-1 |
∴tan45°=
| ||||
1+
|
化简得x2+(y-1)2=2.
∴点P的轨迹方程为x2+(y-1)2=2,
由已知y≥0可得kPA=
| y |
| x+1 |
可知P点的轨迹是以(0,1)为圆心、半径r=
| 2 |
可得轨迹的长度是
| 1 |
| 2 |
| 2 |
故选:B


练习册系列答案
相关题目