题目内容
平面上动点P到定点F（1，0）的距离比P到y轴的距离大1，则动点P的轨迹方程为（ ）
| A．y2=2x | B．y2=4x | ||||||||||
C．y2=2x或
| D．y2=4x或
|
设P（x，y），
由P到定点F（1，0）的距离为
，
P到y轴的距离为|x|，
当x≤0时，P的轨迹为y=0（x≤0）；
当x＞0时，又动点P到定点F（1，0）的距离比P到y轴的距离大1，
列出等式：
-|x|=1
化简得y2=4x （x≥0），为焦点为F（1，0）的抛物线．
则动点P的轨迹方程为y2=4x或
．
故选D．
由P到定点F（1，0）的距离为
| (x-1)2+y2 |
P到y轴的距离为|x|，
当x≤0时，P的轨迹为y=0（x≤0）；
当x＞0时，又动点P到定点F（1，0）的距离比P到y轴的距离大1，
列出等式：
| (x-1)2+y2 |
化简得y2=4x （x≥0），为焦点为F（1，0）的抛物线．
则动点P的轨迹方程为y2=4x或
|
故选D．
练习册系列答案
相关题目
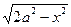,a＞0}，B={(x,y)｜(x–1)2+(y–
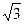)2=a2,a＞0},且A∩B≠
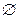，求a的最大值与最小值.