题目内容

已知A（8，0），B、C两点分别在y轴上和x轴上运动，并且满足
AB
•
BP
=0，
BC
=
CP
，
（1）求动点P的轨迹方程；
（2）若过点A的直线l与动点P的轨迹交于M、N两点，
QM
•
QN
=97，其中Q（-1，0），求直线l的方程．
（1）设B（0，b），C（c，0），P（x，y），则
AB
=(-8，b)，
BP
=(x，y-b)，
∴
AB
•
BP
=-8x+b（y-b）=0 ①
由
BC
=
CP
，得（c，-b）=（x-c，y），
∴b=-y，
代入①并化简得，y2=4x；
（2）设l：x=my+8 ②
把②代入y2=4x，整理得
y2-4my-32=0，
设M（x1，y1），N（x2，y2），则
y1+y2=4m，y1y2=-32．
由②得，x1+x2=m(y1+y2)+16=4m2+16，
x1x2=（my1+8）（my2+8）=m2y1y2+8m（y1+y2）+64=64
∴
QM
•
QN
=(x1+1)(x2+1)+y1y2
=x1x2+（x1+x2）+1+y1y2
=64+4m2+16+1-32
=4m2+49=97，
解得：m=土2
3
，
∴l：x土2
3
y-8=0．
练习册系列答案
相关题目
设椭圆C∶＋＝1(a>b>0)过点(0,4)，离心率为.
(1)求C的方程；
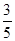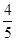(2)求过点(3,0)且斜率为的直线被C所截线段的中点坐标．
对于方程
x2
2
+
y2
m-1
=1（m∈R且m≠1）的曲线C，下列说法错误的是（　　）
A．m＞3时，曲线C是焦点在y轴上的椭圆
B．m=3时，曲线C是圆
C．m＜1时，曲线C是双曲线
D．m＞1时，曲线C是椭圆
如图，在直角坐标系xoy中，AB是半圆O：x2+y2=1（y≥0）的直径，点C是半圆O上任一点，延长AC到点P，使CP=CB，当点C从点B运动到点A时，动点P的轨迹的长度是（　　）
A．2πB．
2
π		C．πD．4
2
π
一条线段的长等于10，两端点A、B分别在x轴和y轴上滑动，M在线段AB上且
AM
=4
MB
，则点M的轨迹方程是（　　）
A．x2+16y2=64B．16x2+y2=64C．x2+16y2=8D．16x2+y2=8
设x，y∈R，若向量
a
=(x，y+2)，
b
=(x，y-2)，且|
a
|-|
b
|=2，则点M（x，y）的轨迹C的方程为______．
若动点P（x1，y1）在曲线y=2x2+1上移动，则点P与点（0，-l）连线中点的轨迹方程为（　　）
A．y=2x2B．y=4x2C．y=6x2D．y=8x2
若△ABC的个顶点坐标A（-4，0）、B（4，0），△ABC的周长为18，则顶点C的轨迹方程为（　　）
A．
x2
25
+
y2
9
=1		B．
y2
25
+
x2
9
=1（y≠0）
C．
x2
16
+
y2
9
=1（y≠0）		D．
x2
25
+
y2
9
=1（y≠0）
已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0．
（1）判断直线l与圆C的位置关系；
（2）设l与圆C交与不同两点A、B，求弦AB的中点M的轨迹方程；
（3）若定点P（1，1）分弦AB为
AP
PB
=
1
2
，求此时直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网