题目内容
两圆x2+y2+2ax+2ay+2a2-1=0与x2+y2+2bx+2by-2=0的公共弦长的最大值是______．
圆x2+y2+2ax+2ay+2a2-1=0化成标准形式，得（x+a）2+（y+a）2=1，
∴该圆表示以M（-a，-a）为圆心，半径为1的圆．
同理圆x2+y2+2bx+2by+2b2-2=0表示以N（-b，-b）为圆心，半径为
的圆．
∵圆M的半径为1，圆N的半径为
，
∴两圆相交于A、B两点，当线段AB恰好为圆M的直径时，公共弦长达到最大值．
即得两圆公共弦长的最大值为2．
故答案为：2
∴该圆表示以M（-a，-a）为圆心，半径为1的圆．
同理圆x2+y2+2bx+2by+2b2-2=0表示以N（-b，-b）为圆心，半径为
| 2 |
∵圆M的半径为1，圆N的半径为
| 2 |
∴两圆相交于A、B两点，当线段AB恰好为圆M的直径时，公共弦长达到最大值．
即得两圆公共弦长的最大值为2．
故答案为：2
练习册系列答案
名校课堂系列答案
相关题目
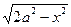,a＞0}，B={(x,y)｜(x–1)2+(y–
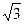)2=a2,a＞0},且A∩B≠
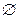，求a的最大值与最小值.
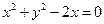和圆O2：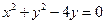
的位置关系是