题目内容
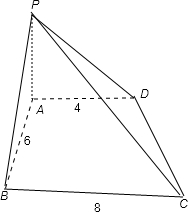
四棱锥P-ABCD中,AD⊥面PAB,BC⊥面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,∠APD=∠CPB,满足上述条件的四棱锥的顶点P的轨迹是( )
| A.圆的一部分 | B.椭圆的一部分 |
| C.球的一部分 | D.抛物线的一部分 |
在平面PAB内,
以AB所在直线为x轴,AB的中垂线为y轴,建立平面直角坐标系.
设点P(x,y),则由题意可得 A(-3,0),B(3,0).
∵AD⊥α,BC⊥α,AD=4,BC=8,AB=6,∠APD=∠CPB,
∴Rt△APD∽Rt△CPB,
∴
=
=
=
.
即 BP2=4AP2,故有(x-3)2+y2=4[(x+3)2+y2],
整理得:(x+5)2+y2=16,表示一个圆.
由于点P不能在直线AB上(否则,不能构成四棱锥),
故点P的轨迹是圆的一部分,
故选A.
以AB所在直线为x轴,AB的中垂线为y轴,建立平面直角坐标系.
设点P(x,y),则由题意可得 A(-3,0),B(3,0).
∵AD⊥α,BC⊥α,AD=4,BC=8,AB=6,∠APD=∠CPB,
∴Rt△APD∽Rt△CPB,
∴
| AP |
| BP |
| AD |
| BC |
| 4 |
| 8 |
| 1 |
| 2 |
即 BP2=4AP2,故有(x-3)2+y2=4[(x+3)2+y2],
整理得:(x+5)2+y2=16,表示一个圆.
由于点P不能在直线AB上(否则,不能构成四棱锥),
故点P的轨迹是圆的一部分,
故选A.


练习册系列答案
相关题目
 +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为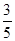 .
.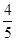 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
 上的点M与椭圆右焦点
上的点M与椭圆右焦点 的连线
的连线 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
 的面积是
的面积是 ,求此时椭圆的方程.
,求此时椭圆的方程.