题目内容
17．若a=log43，b=20.5，c=log2（sin$\frac{π}{3}$），则（ ）| A． | a＞b＞c | B． | a＞c＞b | C． | b＞a＞c | D． | c＞b＞a |
分析 判断三个数与“0”，“1”的大小，推出结果即可．
解答 解：a=log43∈（0，1）；
b=20.5＞1；
c=log2（sin$\frac{π}{3}$）＜0．
∴b＞a＞c．
故选：C．
点评 本题考查数值大小比较，借助中间量是常用方法．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8．|$\overrightarrow a|\;=2，\;\;|\overrightarrow b|\;=1$，$\overrightarrow a$与$\overrightarrow b$之间的夹角为60°，那么向量 $\overrightarrow a-4\;\overrightarrow b$的模为（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | 6 | D． | 12 |
12．
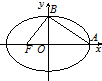如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）
如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）| A． | $\frac{{\sqrt{5}+1}}{2}$ | B． | $\frac{{\sqrt{3}+1}}{2}$ | C． | $\frac{{\sqrt{5}+1}}{3}$ | D． | $\frac{{\sqrt{7}-1}}{2}$ |
2．若2弧度的圆心角所对的弧长为4cm，则这个圆心角所夹的扇形的面积是（ ）
| A． | 2πcm2 | B． | 2 cm2 | C． | 4πcm2 | D． | 4 cm2 |