题目内容
12.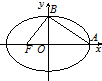 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F(c,0),当$\overrightarrow{AB}⊥\overrightarrow{FB}$时,由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中,由b12=a1c1(c1为黄金双曲线的半焦距)可推出“黄金双曲线”的离心率为( )
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F(c,0),当$\overrightarrow{AB}⊥\overrightarrow{FB}$时,由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中,由b12=a1c1(c1为黄金双曲线的半焦距)可推出“黄金双曲线”的离心率为( )| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | $\frac{{\sqrt{5}+1}}{3}$ | D. | $\frac{{\sqrt{7}-1}}{2}$ |
分析 利用b12=a1c1,可得关于离心率的方程,即可求出“黄金双曲线”的离心率.
解答 解:∵${b_1}^2={a_1}{c_1}$,∴${c_1}^2-{a_1}^2={a_1}{c_1}$,
∴$\frac{{{c_1}^2}}{{{a_1}^2}}-1=\frac{c_1}{a_1}∴{e^2}-e-1=0$,
∴$e=\frac{{\sqrt{5}+1}}{2}$.
故选:A.
点评 本题考查“黄金双曲线”的离心率,考查新定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
20.复数$\frac{(1-i)(1+i)}{i}$在复平面中所对应的点到原点的距离是( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
17.若a=log43,b=20.5,c=log2(sin$\frac{π}{3}$),则( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>b>a |
2.甲乙两人下棋,和棋的概率是$\frac{1}{2}$,乙获胜的概率是$\frac{1}{3}$,则甲不输的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |