题目内容
已知椭圆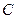 的中心为坐标原点
的中心为坐标原点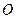 ,一个长轴端点为
,一个长轴端点为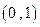 ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线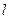 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且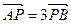 .
.
(1)求椭圆方程;
(2)求m的取值范围.
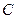 的中心为坐标原点
的中心为坐标原点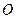 ,一个长轴端点为
,一个长轴端点为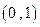 ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且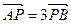 .
.(1)求椭圆方程;
(2)求m的取值范围.
(1)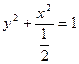 (2)所求m的取值范围为(-1,-
(2)所求m的取值范围为(-1,-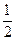 )∪(
)∪(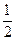 ,1)
,1)
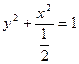 (2)所求m的取值范围为(-1,-
(2)所求m的取值范围为(-1,-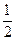 )∪(
)∪(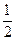 ,1)
,1)【解题思路】通过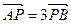 ,沟通A、B两点的坐标关系,再利用判别式和根与系数关系得到一个关于m的不等式。
,沟通A、B两点的坐标关系,再利用判别式和根与系数关系得到一个关于m的不等式。
(1)由题意可知椭圆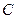 为焦点在
为焦点在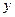 轴上的椭圆,可设
轴上的椭圆,可设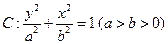
由条件知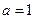 且
且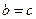 ,又有
,又有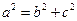 ,解得
,解得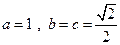
故椭圆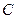 的离心率为
的离心率为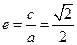 ,其标准方程为:
,其标准方程为: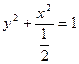
(2)设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=,x1x2=
∵=3∴-x1=3x2∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<-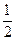 或
或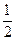 <m<1
<m<1
容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-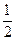 )∪(
)∪(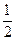 ,1)
,1)
【名师指引】椭圆与向量、解三角形的交汇问题是高考热点之一,应充分重视向量的功能
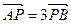 ,沟通A、B两点的坐标关系,再利用判别式和根与系数关系得到一个关于m的不等式。
,沟通A、B两点的坐标关系,再利用判别式和根与系数关系得到一个关于m的不等式。(1)由题意可知椭圆
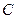 为焦点在
为焦点在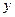 轴上的椭圆,可设
轴上的椭圆,可设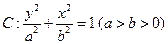
由条件知
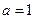 且
且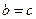 ,又有
,又有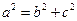 ,解得
,解得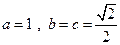
故椭圆
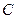 的离心率为
的离心率为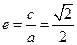 ,其标准方程为:
,其标准方程为: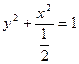
(2)设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=,x1x2=
∵=3∴-x1=3x2∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<-
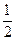 或
或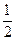 <m<1
<m<1容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-
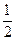 )∪(
)∪(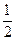 ,1)
,1) 【名师指引】椭圆与向量、解三角形的交汇问题是高考热点之一,应充分重视向量的功能

练习册系列答案
相关题目
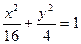 上有两点P、Q ,O为原点,若OP、OQ斜率之积为
上有两点P、Q ,O为原点,若OP、OQ斜率之积为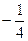 ,则
,则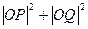 为 ( )
为 ( )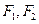 是椭圆
是椭圆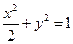 的两个焦点,过
的两个焦点,过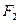 作倾斜角为
作倾斜角为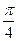 的弦
的弦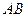 ,得
,得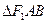 ,求
,求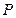 在椭圆
在椭圆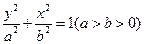 上,
上,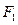 ,
,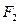 为椭圆的两个焦点,求
为椭圆的两个焦点,求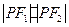 的取值范围.
的取值范围.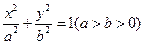 上一点
上一点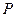 向
向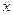 轴引垂线,垂足恰为椭圆的左焦点
轴引垂线,垂足恰为椭圆的左焦点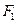 ,
,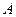 为椭圆的右顶点,
为椭圆的右顶点,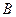 是椭圆的上顶点,且
是椭圆的上顶点,且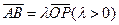 .
.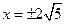 ,求椭圆方程.
,求椭圆方程.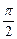 ,则椭圆离心率的范围是_________.
,则椭圆离心率的范围是_________.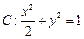 的
的 右焦点为
右焦点为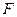 ,右准线为
,右准线为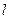 ,点
,点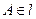 ,线段
,线段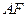 交
交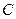 于点
于点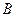 ,若
,若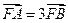 ,则
,则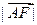 =" " ( )
=" " ( )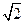
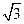
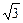 ,求这个椭圆方程.
,求这个椭圆方程.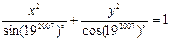 所表示的曲线是( )
所表示的曲线是( )