题目内容
已知椭圆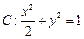 的
的 右焦点为
右焦点为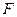 ,右准线为
,右准线为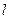 ,点
,点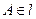 ,线段
,线段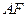 交
交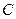 于点
于点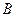 ,若
,若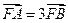 ,则
,则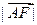 =" " ( )
=" " ( )
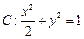 的
的 右焦点为
右焦点为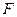 ,右准线为
,右准线为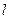 ,点
,点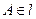 ,线段
,线段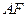 交
交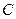 于点
于点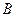 ,若
,若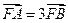 ,则
,则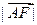 =" " ( )
=" " ( )A.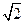 | B.2 | C.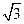 | D.3 |
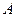
过点B作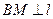 于M,并设右准线
于M,并设右准线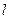 与x轴的交点为N,易知FN=1.由题意
与x轴的交点为N,易知FN=1.由题意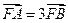 ,故
,故 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得 ,
,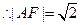 .
.
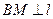 于M,并设右准线
于M,并设右准线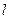 与x轴的交点为N,易知FN=1.由题意
与x轴的交点为N,易知FN=1.由题意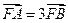 ,故
,故 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得 ,
,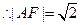 .
.
练习册系列答案
相关题目
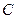 的中心为坐标原点
的中心为坐标原点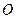 ,一个长轴端点为
,一个长轴端点为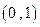 ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且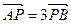 .
. 的椭圆方程.
的椭圆方程.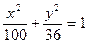
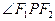
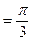 ,则
,则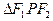 的面积是 。
的面积是 。

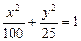 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以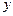 轴为对称轴、
轴为对称轴、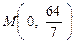 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为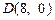 . 观测点
. 观测点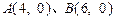 同时跟踪航天器.求航天器变轨后的运行轨迹所在的曲线方程。
同时跟踪航天器.求航天器变轨后的运行轨迹所在的曲线方程。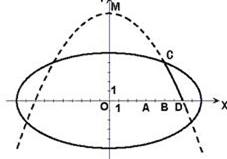
 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是椭圆上任意一点,求
是椭圆上任意一点,求 的最大值和最小值。
的最大值和最小值。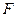 是椭圆的左焦点,
是椭圆的左焦点,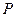 是椭圆上一点,
是椭圆上一点,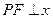 轴,
轴,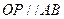 ,
, 求椭圆的离心率。
求椭圆的离心率。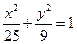 上一点到两焦点的距离之积为
上一点到两焦点的距离之积为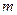 ,求
,求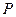 点的坐标。
点的坐标。