题目内容
12．
用一个边长为2$\sqrt{2}$的正方形硬纸板，按各边中点垂直折起四个小三角形，做成一个蛋巢，半径为2的鸡蛋（视为球体）放入其中，则鸡蛋中心（球心）与蛋巢底面的距离为（ ）| A． | $\sqrt{3}+1$ | B． | 1 | C． | $\sqrt{2}+1$ | D． | 3 |
分析 蛋槽的边长是原来硬纸板的对角线长度的一半，为2，蛋槽立起来的小三角形部分高度是1，鸡蛋的半径为2，直径为4，大于折好的蛋巢边长2，由此能求出鸡蛋中心（球心）与蛋巢底面的距离．
解答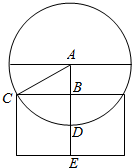 
解：蛋槽的边长是原来硬纸板的对角线长度的一半，为2，
蛋槽立起来的小三角形部分高度是1，
鸡蛋的半径为2，直径为4，大于折好的蛋巢边长2，四个三角形的顶点所在的平面在鸡蛋表面所截取的小圆直径就是蛋槽的边长2，
根据图示，AB段由三角形AB求出得：AB=$\sqrt{3}$，
AE=AB+BE=$\sqrt{3}$+1，
∴鸡蛋中心（球心）与蛋巢底面的距离为$\sqrt{3}$+1．
故选：A．
点评 本题考查点、线、面间距离的计算，解题时要认真审题，注意挖掘题设中的隐含条件，合理地化空间问题为平面问题，注意数形结合法的合理运用．
练习册系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
20．从A，B，C，D，E5名学生中选出4名分别参加数学、物理、化学、外语竞赛，其中A不参加物理、化学竞赛，则不同的参赛方案种数为（ ）
| A． | 24 | B． | 48 | C． | 72 | D． | 120 |
7．已知全集U=R，集合A={x|y=log2（x2+3x-10）}，B={x|-2≤x≤5}，则（∁UA）∩B等于（ ）
| A． | {x|-5＜x≤2} | B． | {x|-2＜x≤5} | C． | {x|-2≤x≤2} | D． | {x|-5≤x≤5} |
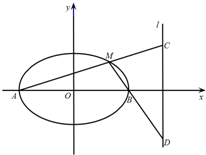已知椭圆G：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，过其右焦点与长轴垂直的弦长为1，如图，A，B是椭圆的左右顶点，M是椭圆上位于x轴上方的动点，直线AM，BM与直线l：x=4分别交于C，D两点．
1．终边在y轴的非负半轴上的角的集合是（ ）
| A． | {x|x=k•180°，k∈Z} | B． | {x|x=k•180°+90°，k∈Z} | ||
| C． | {x|x=k•360°，k∈Z} | D． | {x|x=k•360°+90°，k∈Z} |