题目内容
19.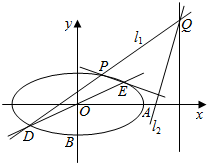 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过点A(a,0)与B(0,-b)的直线与原点的距离为$\frac{2\sqrt{10}}{5}$,又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点,过D点作斜率为k的直线l1与椭圆C的另一个交点为P,与直线x=4的交点为Q,过Q点作直线EP的垂线l2.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过点A(a,0)与B(0,-b)的直线与原点的距离为$\frac{2\sqrt{10}}{5}$,又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点,过D点作斜率为k的直线l1与椭圆C的另一个交点为P,与直线x=4的交点为Q,过Q点作直线EP的垂线l2.(1)求椭圆的方程;
(2)求证:直线l2恒过一定点.
分析 (1)过点A(a,0)与B(0,-b)的直线方程为:$\frac{x}{a}+\frac{y}{-b}=1$.根据此直线与原点的距离为$\frac{2\sqrt{10}}{5}$,可得$\frac{ab}{\sqrt{{b}^{2}+(-a)^{2}}}$=$\frac{2\sqrt{10}}{5}$,联立$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{8{a}^{2}+8{b}^{2}=5{a}^{2}{b}^{2}}\end{array}\right.$,解得即可得出.
(2)联立$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{{x}^{2}+4{y}^{2}=8}\end{array}\right.$,解得D(-2,-1),E(2,1).可得直线l1的方程为:y+1=k(x+2),与x=4联立可得Q(4,6k-1).联立$\left\{\begin{array}{l}{y=kx+2k-1}\\{{x}^{2}+4{y}^{2}=8}\end{array}\right.$,利用根与系数的关系可得:P$(\frac{-8{k}^{2}+8k+2}{1+4{k}^{2}},\frac{4{k}^{2}+4k-1}{1+4{k}^{2}})$,可得kEP=-$\frac{1}{4k}$.利用相互垂直的直线斜率之间的关系可得${k}_{{l}_{2}}$=4k.直线l2的方程为:y-(6k-1)=4k(x-4),利用直线系即可得出此直线过定点.
解答 (1)解:过点A(a,0)与B(0,-b)的直线方程为:$\frac{x}{a}+\frac{y}{-b}=1$,化为bx-ay-ab=0.
∵此直线与原点的距离为$\frac{2\sqrt{10}}{5}$,∴$\frac{ab}{\sqrt{{b}^{2}+(-a)^{2}}}$=$\frac{2\sqrt{10}}{5}$,化为8a2+8b2=5a2b2.
联立$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{8{a}^{2}+8{b}^{2}=5{a}^{2}{b}^{2}}\end{array}\right.$,解得b2=2,a2=8,$c=\sqrt{6}$.
∴椭圆的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$.
(2)证明:联立$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{{x}^{2}+4{y}^{2}=8}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,
∴D(-2,-1),E(2,1).
∴直线l1的方程为:y+1=k(x+2),
把x=4代入可得y=6k-1,∴Q(4,6k-1).
联立$\left\{\begin{array}{l}{y=kx+2k-1}\\{{x}^{2}+4{y}^{2}=8}\end{array}\right.$,化为(1+4k2)x2+(16k2-8k)x+16k2-16k-4=0,
则-2×xP=$\frac{16{k}^{2}-16k-4}{1+4{k}^{2}}$,解得xP=$\frac{-8{k}^{2}+8k+2}{1+4{k}^{2}}$,yP=$\frac{4{k}^{2}+4k-1}{1+4{k}^{2}}$.
解得P$(\frac{-8{k}^{2}+8k+2}{1+4{k}^{2}},\frac{4{k}^{2}+4k-1}{1+4{k}^{2}})$,
∴kEP=$\frac{\frac{4{k}^{2}+4k-1}{1+4{k}^{2}}-1}{\frac{-8{k}^{2}+8k+2}{1+4{k}^{2}}-2}$=-$\frac{1}{4k}$.
∴${k}_{{l}_{2}}$=4k.
∴直线l2的方程为:y-(6k-1)=4k(x-4),
化为k(4x-10)-(y+1)=0,
令$\left\{\begin{array}{l}{4x-10=0}\\{y+1=0}\end{array}\right.$,解得x=$\frac{5}{2}$,y=-1.
∴直线l2恒过一定点$(\frac{5}{2},-1)$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题、斜率计算公式、相互垂直的直线斜率之间的关系、直线系的应用、点到直线的距离公式,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | 1100(2) | B. | 1011(2) | C. | 110(2) | D. | 1110(2) |