题目内容
14．已知A={x|ax2+2x-3a=0}，B={x|ax-1=0}，是否存在实数a使A=B，若存在，求出a；若不存在，说明理由．分析 根据集合相等的条件进行求解即可．
解答 解：若a=0，则A={x|2x=0}={0}，B={x|ax-1=0}={x|-1=0}=∅，不满足条件A=B，
若a≠0，则b={x|ax-1=0}={$\frac{1}{a}$}，
若A=B，
则A={$\frac{1}{a}$}，
则判别式△=4+12a2=0，∵a≠0，∴4+12a2=0不成立，
即不存在实数a使A=B．
点评 本题主要考查集合相等的应用，结合一元二次方程和一元一次方程根的关系是解决本题的关键．
练习册系列答案
相关题目
4．函数y=$\frac{x}{\sqrt{（x+2）（x-2）}}$的定义域是（ ）
| A． | {x|-2＜x＜2} | B． | {x|x＞2} | C． | {x|-2＜x＜0，或0＜x＜2} | D． | {x|x＞2，或x＜-2} |
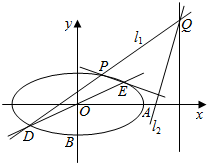如图，在直角坐标系xOy中，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，过点A（a，0）与B（0，-b）的直线与原点的距离为$\frac{2\sqrt{10}}{5}$，又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点，过D点作斜率为k的直线l1与椭圆C的另一个交点为P，与直线x=4的交点为Q，过Q点作直线EP的垂线l2．