题目内容
4.(1)已知f($\frac{1+x}{x}$)=$\frac{1+{x}^{2}}{{x}^{2}}$+$\frac{1}{x}$,求f(x)的解析式.(2)已知函数f(x)满足f(x)-2f($\frac{1}{x}$)=x,求函数f(x)的解析式.
分析 (1)已知解析式变形为f(1+$\frac{1}{x}$)=(1+$\frac{1}{x}$)2-(1+$\frac{1}{x}$)+1,用x替换式中的1+$\frac{1}{x}$可得f(x)的解析式;
(2)由f(x)-2f($\frac{1}{x}$)=x可得f($\frac{1}{x}$)-2f(x)=$\frac{1}{x}$,联立消去f($\frac{1}{x}$)可得f(x).
解答 解:(1)f($\frac{1+x}{x}$)=$\frac{1+{x}^{2}}{{x}^{2}}$+$\frac{1}{x}$可化为f(1+$\frac{1}{x}$)=1+$\frac{1}{x}$+$\frac{1}{{x}^{2}}$,
即f(1+$\frac{1}{x}$)=(1+$\frac{1}{x}$)2-(1+$\frac{1}{x}$)+1,
∴f(x)的解析式为f(x)=x2-x+1;
(2)∵f(x)-2f($\frac{1}{x}$)=x,∴f($\frac{1}{x}$)-2f(x)=$\frac{1}{x}$,
联立消去f($\frac{1}{x}$)可得f(x)=-$\frac{x}{3}$-$\frac{2}{3x}$,
∴函数f(x)的解析式为f(x)=-$\frac{x}{3}$-$\frac{2}{3x}$.
点评 本题考查函数解析式求解的配凑法和方程组的方法,属中档题.

练习册系列答案
相关题目
14.已知△ABC的面积S=$\frac{\sqrt{3}}{4}$(a2+b2-c2),则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
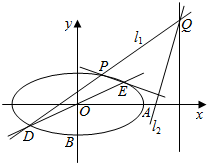 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过点A(a,0)与B(0,-b)的直线与原点的距离为$\frac{2\sqrt{10}}{5}$,又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点,过D点作斜率为k的直线l1与椭圆C的另一个交点为P,与直线x=4的交点为Q,过Q点作直线EP的垂线l2.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过点A(a,0)与B(0,-b)的直线与原点的距离为$\frac{2\sqrt{10}}{5}$,又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点,过D点作斜率为k的直线l1与椭圆C的另一个交点为P,与直线x=4的交点为Q,过Q点作直线EP的垂线l2.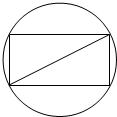 如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?