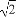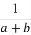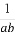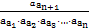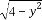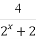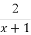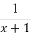题目内容
若集合A1,A2,…,An满足A1∪A2∪…∪An=A,则称A1,A2,…,An为集合A的一种拆分.已知:
①当A1∪A2={a1,a2,a3}时,有33种拆分;
②当A1∪A2∪A3={a1,a2,a3,a4}时,有74种拆分;
③当A1∪A2∪A3∪A4={a1,a2,a3,a4,a5}时,有155种拆分;
……
由以上结论,推测出一般结论:
当A1∪A2∪…∪An={a1,a2,a3,…,an+1}时,有 种拆分.
(2n-1)n+1
【解析】因为当有两个集合时,
33=(4-1)2+1=(22-1)2+1;当有三个集合时,74=(8-1)3+1=(23-1)3+1;当有四个集合时,155=(16-1)4+1=(24-1)4+1;由此可以归纳当有n个集合时,有(2n-1)n+1种拆分.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目