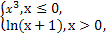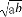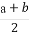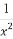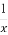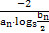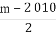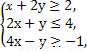题目内容
若 <
< <0,则下列不等式:①
<0,则下列不等式:①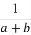 <
<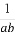 ;②|a|+b>0;③a-
;②|a|+b>0;③a- >b-
>b- ;④lna2>lnb2中,正确的是( )
;④lna2>lnb2中,正确的是( )
(A)①④ (B)②③ (C)①③ (D)②④
D
【解析】先由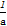 <
<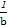 <0得到a与b的大小关系,再根据不等式的性质,对各个不等式进行逐一判断.
<0得到a与b的大小关系,再根据不等式的性质,对各个不等式进行逐一判断.
由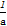 <
<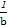 <0,可知b<a<0.
<0,可知b<a<0.
①中,a+b<0,ab>0,所以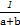 <0,
<0,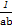 >0.
>0.
故有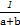 <
<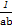 ,即①正确.
,即①正确.
②中,∵b<a<0,∴-b>-a>0,故-b>|a|,即|a|+b<0,故②错误.
③中,∵b<a<0,即0>a>b,
又∵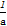 <
<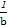 <0,∴-
<0,∴-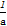 >-
>-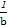 >0,
>0,
∴a-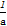 >b-
>b-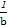 ,故③正确.
,故③正确.
④中,∵b<a<0,根据y=x2在(-∞,0)上为单调递减函数,可得b2>a2>0,而y=lnx在定义域上为增函数.∴lnb2>lna2,故④错,综上分析,②④错误,①③正确.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目