题目内容
【题目】(导学号:05856287)
已知点A(0,1)与B(![]() ,
, ![]() )都在椭圆C:
)都在椭圆C: ![]() (a>b>0)上,直线AB交x轴于点M.
(a>b>0)上,直线AB交x轴于点M.
(Ⅰ)求椭圆C的方程,并求点M的坐标;
(Ⅱ)设O为原点,点D与点B关于x轴对称,直线AD交x轴于点N.问:y轴上是否存在点E,使得∠OEM=∠ONE?若存在,求点E的坐标;若不存在,说明理由.
【答案】(1) ![]() +y2=1. 点M(
+y2=1. 点M(![]() ,0) (2) 在y轴上存在点E,使得∠OEM=∠ONE,且点E的坐标为(0,2)或(0,-2).
,0) (2) 在y轴上存在点E,使得∠OEM=∠ONE,且点E的坐标为(0,2)或(0,-2).
【解析】试题分析:(1)由点A(0,1)与B(![]() ,
, ![]() )都在椭圆C:
)都在椭圆C: ![]() (a>b>0)上,利用待定系数法能求出椭圆C的方程和直线AB的方程,由此能求出点M的坐标.
(a>b>0)上,利用待定系数法能求出椭圆C的方程和直线AB的方程,由此能求出点M的坐标.
(2)由已知求出D(![]() ,﹣
,﹣![]() ),直线AD:3x+2
),直线AD:3x+2![]() y﹣2
y﹣2![]() =0,从而求出N(
=0,从而求出N(![]() ,0),设E(0,y0),由∠OEM=∠ONE,得到|
,0),设E(0,y0),由∠OEM=∠ONE,得到|![]() |=|
|=|![]() |,从而求出y轴上是否存在点E(±2,0),使得∠OEM=∠ONE.
|,从而求出y轴上是否存在点E(±2,0),使得∠OEM=∠ONE.
试题解析:
(Ⅰ)由题意得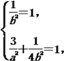 ∴
∴![]()
故椭圆C的方程为![]() +y2=1.
+y2=1.
直线AB方程为y=-![]() x+1,与x轴交于点M(2
x+1,与x轴交于点M(2![]() ,0).
,0).
(Ⅱ)因为点D与点B关于x轴对称,
所以D(![]() ,-),
,-),
直线AD方程为y=-![]() x+1,
x+1,
与x轴交点N(![]() ,0).
,0).
“存在点E(0,yE)使得∠OEM=∠ONE”等价于“存在点E(0,yE)使得![]() =
=![]() ”,
”,
即yE满足y=|xM||xN|.
∴y=2![]() ×
×![]() =4,∴yE=±2,
=4,∴yE=±2,
故在y轴上存在点E,使得∠OEM=∠ONE,且点E的坐标为(0,2)或(0,-2).

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目