Question

【题目】已知椭圆C： (a>b>0)过点(1， )，且离心率e＝.

(Ⅰ)求椭圆C的标准方程；

(Ⅱ)若直线l：y＝kx＋m与椭圆C相交于A，B两点(A，B不是左右顶点)，椭圆的右顶点为D，且满足·＝0，试判断直线l是否过定点，若过定点，求出该定点的坐标；若不过定点，请说明理由．

Answer 1

【答案】(1) (2) 直线过定点(，0)

【解析】试题分析：（Ⅰ）由e＝可得，利用，把点(1， )代入椭圆方程，即可得出椭圆C的标准方程；（Ⅱ）设A(x1，y1)，B(x2，y2)，联立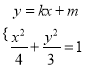，得到根与系数的关系，利用，得到kAD·kBD＝－1，即可得出结论.

试题解析：(Ⅰ)由题意椭圆的离心率e＝.

∴

∴a＝2c

∴b2＝a2－c2＝3c2

∴椭圆方程为

又∵点(1， )在椭圆上

∴

∴c2＝1

∴椭圆的方程为

(Ⅱ)设A(x1，y1)，B(x2，y2)，由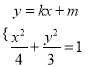得(3＋4k2)x2＋8mkx＋4(m2－3)＝0，

Δ＝64m2k2－16(3＋4k2)(m2－3)>0,3＋4k2－m2>0，则x1＋x2＝，x1·x2＝

∴y1·y2＝(kx1＋m)·(kx2＋m)＝k2x1x2＋mk(x1＋x2)＋m2＝

∵

∴kAD·kBD＝－1

又∵椭圆的右顶点D(2,0)，

∴，则y1y2＋x1x2－2(x1＋x2)＋4＝0

，7m2＋16mk＋4k2＝0，解得

m1＝－2k，m2＝，且满足3＋4k2－m2>0

当m＝－2k时，l：y＝k(x－2)，直线过定点(2,0)与已知矛盾；

当m＝时，l：y＝k(x)，直线过定点(，0)．

综上可知，直线l过定点，定点坐标为(，0).