题目内容
【题目】已知抛物线C; y2 =2x的焦点为F,准线为l, P为抛物线C上异于顶点的动点.
(1)过点P作准线1的垂线,垂足为H,若△PHF与△POF的面积之比为2:1,求点P的坐标;
(2)过点M(![]() ,0)任作一条直线 m与抛物线C交于不同的两点A, B.若两直线PA, PB 斜率之和为2,求点P的坐标.
,0)任作一条直线 m与抛物线C交于不同的两点A, B.若两直线PA, PB 斜率之和为2,求点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)求得抛物线的焦点和准线,设![]() ,
,![]() ,由三角形的面积公式可得
,由三角形的面积公式可得![]() ,解方程可得
,解方程可得![]() ,进而可得
,进而可得![]() 的坐标;
的坐标;
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立抛物线的方程,消去
,联立抛物线的方程,消去![]() ,可得
,可得![]() 的二次方程,设
的二次方程,设![]() ,
,![]() ,
,![]() ,
,![]() ,运用韦达定理和判别式大于0,再由直线的斜率公式,化简整理可得
,运用韦达定理和判别式大于0,再由直线的斜率公式,化简整理可得![]() ,
,![]() 的方程,由恒成立思想可得
的方程,由恒成立思想可得![]() ,进而得到所求
,进而得到所求![]() 的坐标,
的坐标,
解:(1)抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,准线为
,准线为![]() ,
,
设![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,
,
由![]() ,与
,与![]() 的面积之比为
的面积之比为![]() ,可得
,可得![]() ,
,
即为![]() ,解得
,解得![]() ,则
,则![]() 的坐标为
的坐标为![]() ,
,![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立抛物线方程可得
,联立抛物线方程可得![]() ,
,
由△![]() ,即
,即![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
则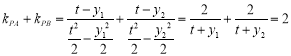 ,
,
化为![]() ,
,
即![]() ,可得
,可得![]() 对满足条件的
对满足条件的![]() 恒成立,
恒成立,
可得![]() ,则
,则![]() 的坐标为
的坐标为![]() ,
,![]() .
.

练习册系列答案
相关题目