题目内容
【题目】已知
、
、
、
与
、
、
、
是8个不同的实数，若方程
有有限多个解，则此方程的解最多有________个.
【答案】4
【解析】
设a1＜a2＜a3＜a4与b1＜b2＜b3＜b4，设函数y＝|x﹣a1|+|x﹣a2|+|x﹣a3|+x﹣a4|，y＝|x﹣b1|+|x﹣b2|+|x﹣b3|+x﹣b4|，去绝对值，讨论平行和交点的情况，即可得到所求个数．
解：a1，a2，a3，a4与b1，b2，b3，b4是8个不同的实数，
且a1＜a2＜a3＜a4与b1＜b2＜b3＜b4，
设函数y＝|x﹣a1|+|x﹣a2|+|x﹣a3|+x﹣a4|，
可得x≤a1，y＝a1+a2+a3+a4﹣4x；
a1＜x≤a2，y＝﹣a1+a2+a3+a4﹣2x；
a2＜x≤a3，y＝﹣a1﹣a2+a3+a4；
a3＜x≤a4，y＝﹣a1﹣a2﹣a3+a4+2x；
x＞a4，y＝﹣a1﹣a2﹣a3﹣a4+4x；
同理可得，设函数y＝|x﹣b1|+|x﹣b2|+|x﹣b3|+x﹣b4|，
可得x≤b1，y＝b1+b2+b3+b4﹣4x；
b1＜x≤b2，y＝﹣b1+b2+b3+b4﹣2x；
b2＜x≤b3，y＝﹣b1﹣b2+b3+b4；
b3＜x≤b4，y＝﹣b1﹣b2﹣b3+b4+2x；
x＞b4，y＝﹣b1﹣b2﹣b3﹣b4+4x；
作出二者的图象，
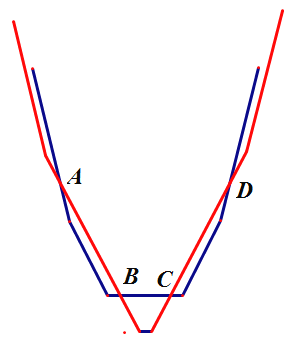
由图象可知二者最多有4个交点，
故答案为：4．
练习册系列答案
相关题目
