题目内容
【题目】三棱锥![]() 中,底面
中,底面![]() 满足
满足![]() ,
,![]() ,
,![]() 在面
在面![]() 的射影为
的射影为![]() 的中点,且该三棱锥的体积为
的中点,且该三棱锥的体积为![]() ,当其外接球的表面积最小时,P到面ABC的距离为_______.
,当其外接球的表面积最小时,P到面ABC的距离为_______.
【答案】3
【解析】
设AB=a,棱锥的高为h,根据体积得出a与h的关系,根据勾股定理得出外接球半径R关于h的表达式,利用基本不等式得出R最小值时对应的h的值即可.
解:设AC的中点为D,连接BD,PD,则PD⊥平面ABC,
∵△ABC是等腰直角三角形,∴外接球的球心O在PD上,

设AB=BC=a,PD=h,外接球半径OC=OP=R,
则OD=![]() ,CD
,CD![]() AC
AC![]() a,
a,
∵VP﹣ABC![]() ,∴a2
,∴a2![]() ,
,
∵CD2+OD2=OC2,即(h﹣R)2![]() a2=R2,
a2=R2,
∴R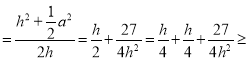 3
3![]() ,
,
当且仅当![]() 即h=3时取等号,
即h=3时取等号,
∴当外接球半径取得最小值时,h=3.
故答案为:3.

练习册系列答案
相关题目
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()