题目内容
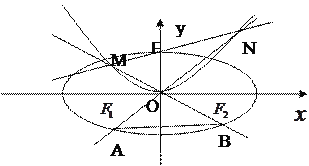
【题目】已知抛物线E∶y2=2px(p>0)的焦点为F,过F且斜率为1的直线交E于A,B两点,线段AB的中点为M,其垂直平分线交x轴于点C,MN⊥y轴于点N.若四边形CMNF的面积等于7,则E的方程为( )
A.y2=xB.y2=2x
C.y2=4xD.y2=8x
【答案】C
【解析】
联立方程组求出各点的坐标,根据四边形CMNF的面积等于![]() ,求得
,求得![]() 的值,即可得到抛物线的方程,得到答案.
的值,即可得到抛物线的方程,得到答案.
由题意知F![]() ,则直线AB的方程为y=x-
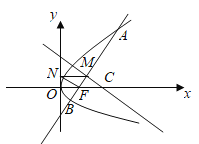
,则直线AB的方程为y=x-![]() .如图,四边形CMNF为梯形,且MN∥FC,
.如图,四边形CMNF为梯形,且MN∥FC,
设A(x1,y1),B(x2,y2),由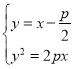 得y2-2py-p2=0,所以y1+y2=2p,
得y2-2py-p2=0,所以y1+y2=2p,
所以x1+x2=y1+y2+p=3p,所以xM=![]() =
=![]() ,yM=
,yM=![]() =p,
=p,
因为MC⊥AB,所以kMC=-1,
所以直线MC的方程为y-p=-![]() ,即y=-x+
,即y=-x+![]() ,所以xC=
,所以xC=![]() ,
,
所以四边形CMNF的面积为![]() (xM+|FC|)·yM=
(xM+|FC|)·yM=![]() ·p=7,得p=2,
·p=7,得p=2,
所以抛物线E的方程为y2=4x,
故选:C.

练习册系列答案
相关题目