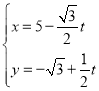Question

【题目】某射击小组有甲、乙、丙三名射手，已知甲击中目标的概率是，甲、丙二人都没有击中目标的概率是，乙、丙二人都击中目标的概率是.甲乙丙是否击中目标相互独立.

（1）求乙、丙二人各自击中目标的概率；

（2）设乙、丙二人中击中目标的人数为X，求X的分布列和数学期望.

Answer 1

【答案】（1），.（2）分布列见解析，数学期望.

【解析】

（1）设甲、乙、丙击中目标分别记为事件，则，且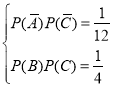，由此能求出乙、丙二人各自击中目标的概率．
（2）由题意X的可能取值为0，1，2，分别求出相应的概率，由此能求出X的分布列和E（X）．

解：（1）设甲、乙、丙击中目标分别记为事件A、B、C，则，且有

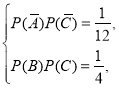即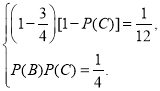

解得，，

所以乙、丙二人各自击中目标的概率分别为，；

（2）由题意，X的可能取值为0，1，2，

，

，

.

所以随机变量X的分布列为

X	0	1	2
P

所以X的数学期望为.