题目内容
【题目】设两个向量![]() ,
,![]() 满足|
满足|![]() |=2,|
|=2,|![]() |=1,
|=1,![]() ,
,![]() 的夹角为60°,若向量2t
的夹角为60°,若向量2t![]() 7
7![]() 与向量
与向量![]() t
t![]() 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
【答案】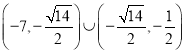 .
.
【解析】
设出向量夹角为θ,结合向量夹角是钝角,得cosθ<0,且cosθ≠﹣1,即2t2+15t+7<0,且![]() ,由此求得实数t的取值范围.
,由此求得实数t的取值范围.
由题意可得 ![]() 2×1×cos60°=1,
2×1×cos60°=1,
设向量2t![]() 7
7![]() 与向量
与向量![]() t
t![]() 的夹角为θ,
的夹角为θ,
则θ∈(90°,180°),则有 cosθ<0,且 cosθ≠﹣1.
即2t![]() 7
7![]() 与向量
与向量![]() t
t![]() 的不能反向共线,且向量数量积(2t
的不能反向共线,且向量数量积(2t![]() 7
7![]() )(
)(![]() t
t![]() )<0,
)<0,
设![]() k(
k(![]() ),(k>0),则
),(k>0),则![]() .得t=±
.得t=±![]() ,
,
由(2t![]() 7
7![]() )(
)(![]() t
t![]() )<0,得2t
)<0,得2t![]() 2+7t/span>
2+7t/span>![]() 2+(2t2+7)
2+(2t2+7)![]()
![]() 0,
0,
∴2t2+15t+7<0,
解得 ![]() 且t=±
且t=±![]() ,
,
故实数t的取值范围为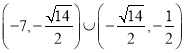 .
.

练习册系列答案
相关题目