题目内容
直线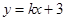
与圆
相交于M,N两点，若
，则k的取值范围是（ ）
A． | B． |
C． | D． |
A
解析试题分析：由弦长公式得，当圆心到直线的距离等于1时，弦长等于2
，故当弦长大于或等于2 时，圆心到直线的距离小于或等于1，解此不等式求出k的取值范围．解：设圆心（3，2）到直线y=kx+3的距离为d，由弦长公式得，MN=
，故可知元新的奥直线的距离d
，即可知为
，故答案为
考点：直线与圆位置关系
点评：本题主要考查点到直线的距离公式，以及弦长公式的应用，属于中档题．
练习册系列答案
相关题目
若直线
与圆
相切，则
的值是 （ ）
A．1， | B．2， | C．1 | D． |
过点
与圆
相交的所有直线中，被圆截得的弦最长的直线方程是（ ）
A． | B． | C． | D． |
设直线
与圆
相交于
点，则弦
的长等于( )
A． | B． | C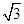． | D．1 |
若直线
与圆
的两个交点关于直线
对称，则
的值分别为
A． | B． |
C． | D． |
圆C1 :(x+1)2+(y+4)2=16与圆C2 : (x-2)2+(y+2)2=9的位置关系是( )．
| A．相交 | B．外切 | C．内切 | D．相离 |
若圆C：(x＋1)2＋(y－1)2＝8上有且只有两个点到直线x＋y＋m＝0的距离等于
，则实数m的取值范围是( )．
| A．(－8，－4)∪(4,8) | B．(－6，－2)∪(2,6) |
| C．(2,6) | D．(4,8) |
若实数x，y满足x²+y²-2x+4y=0，则x-2y的最大值为 ( )
A． | B．10 | C．9 | D．5+2 |
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域（含边界），A、B、C、D是该圆的四等分点，若点P(x,y)、
，则称P优于
，如果