题目内容
若圆C:(x+1)2+(y-1)2=8上有且只有两个点到直线x+y+m=0的距离等于 ,则实数m的取值范围是( ).
,则实数m的取值范围是( ).
| A.(-8,-4)∪(4,8) | B.(-6,-2)∪(2,6) |
| C.(2,6) | D.(4,8) |
B
解析试题分析:设圆心(-1,1)到直线x+y+m=0的距离为d,则由题意可得r- <d<r+
<d<r+ .
.
即 <
<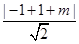 <3
<3 ,解得 2<m<6或-6<m<-2,故选B.
,解得 2<m<6或-6<m<-2,故选B.
考点:直线和圆的位置关系,点到直线的距离公式,绝对值不等式解法。
点评:小综合题,根据点到直线的距离公式及已知条件,建立m的不等式,进一步求解。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
直线 与圆
与圆 的位置关系是 ( )
的位置关系是 ( )
| A.相交 | B.相切 | C.相离 | D.取决于 的值 的值 |
已知直线 与圆
与圆 相切,若对任意的
相切,若对任意的 均有不等式
均有不等式 成立,那么正整数
成立,那么正整数 的最大值是( )
的最大值是( )
| A.3 | B.5 | C.7 | D.9 |
直线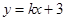 与圆
与圆 相交于M,N两点,若
相交于M,N两点,若 ,则k的取值范围是( )
,则k的取值范围是( )
A. | B. |
C. | D. |
若方程 的任意一组解
的任意一组解 都满足不等式
都满足不等式 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D.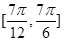 |
已知圆C1: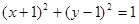 ,圆C2与圆C1关于直线
,圆C2与圆C1关于直线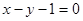 对称,则圆C2的方程为
对称,则圆C2的方程为
A.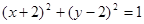 | B.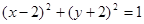 |
C.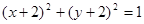 | D.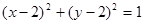 |
已知两点 到直线
到直线 的距离分别为
的距离分别为 ,则满足条件的直线
,则满足条件的直线 共有( )条
共有( )条
| A.1 | B.2 | C.3 | D.4 |
如果圆x2+y2+Dx+Ey+F=0与x轴切于原点, 那么( )
| A.D=0,E≠0, F≠0 | B.E=F=0,D≠0 | C.D="F=0," E≠0 | D.D=E=0,F≠0 |
若直线 与圆
与圆 有公共点,则实数
有公共点,则实数 取值范围是( )
取值范围是( )
A. | B. |
C. | D. |