题目内容
若直线
与圆
相切，则
的值是 （ ）
A．1， | B．2， | C．1 | D． |
D
解析试题分析：将圆的方程化为标准方程得
，圆心坐标为
，半径为
，由于直线
与圆相切，则有
，即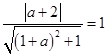
，
化简得
.
考点：直线与圆的位置关系
练习册系列答案
相关题目
两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线
相切，则a的取值范围是（ ）
A． | B． |
C．-3≤a≤一 或≤a≤7 | D．a≥7或a≤—3 |
圆
的圆心坐标和半径分别是（ ）
| A．（0，2）2 | B．（2，0）4 | C．（－2，0）2 | D．（2，0）2 |
若当方程
所表示的圆取得最大面积时，则直线
的倾斜角
（ ）．
A． | B． | C． | D． |
若直线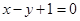
与圆
有公共点，则实数
取值范围是（ ）
A． | B． |
C． | D． |
圆
在点
处的切线方程为（ ）
A． | B． |
C． | D． |
直线
与圆
的位置关系是 （ ）
| A．相交 | B．相切 | C．相离 | D．取决于 的值 |
自点 
的切线，则切线长为（ ）
A． | B．3 | C． | D．5 |
直线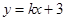
与圆
相交于M,N两点，若
，则k的取值范围是（ ）
A． | B． |
C． | D． |