题目内容
(本小题满分12分)设函数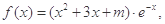 (其中
(其中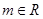 ,
,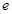 是自然对数的底数)
是自然对数的底数)
(I)若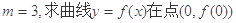 处的切线方程;
处的切线方程;
(II)若函数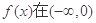 上有两个极值点.
上有两个极值点.
①实数m的范围; ②证明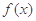 的极小值大于e.
的极小值大于e.
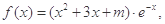 (其中
(其中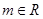 ,
,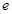 是自然对数的底数)
是自然对数的底数)(I)若
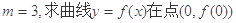 处的切线方程;
处的切线方程;(II)若函数
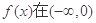 上有两个极值点.
上有两个极值点.①实数m的范围; ②证明
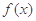 的极小值大于e.
的极小值大于e.解:(I)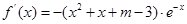 ∵m=3
∵m=3
∴ ,
,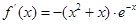 ∴
∴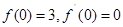
故曲线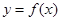 在点(0,
在点(0, )处的切线方程为:y=3 4分
)处的切线方程为:y=3 4分
(II)由(I)知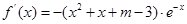 ,要使函数
,要使函数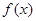 在
在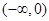 有两个极值点,只要方程
有两个极值点,只要方程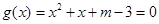 有两个不等负根,那么实数m应满足
有两个不等负根,那么实数m应满足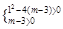 ,解得
,解得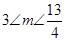 8分
8分
设两负根为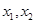 ,则
,则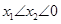 ,可只当
,可只当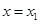 时有极小值
时有极小值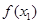 ,由于对称轴为
,由于对称轴为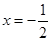 ,
,
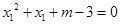 ,
,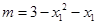
∴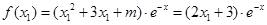 ,
,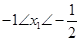 ,
,
 ∵
∵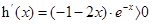
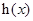 在
在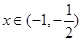 上单调递增
上单调递增
∴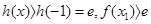
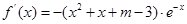 ∵m=3
∵m=3∴
 ,
,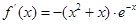 ∴
∴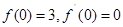
故曲线
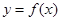 在点(0,
在点(0, )处的切线方程为:y=3 4分
)处的切线方程为:y=3 4分(II)由(I)知
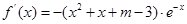 ,要使函数
,要使函数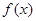 在
在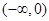 有两个极值点,只要方程
有两个极值点,只要方程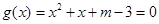 有两个不等负根,那么实数m应满足
有两个不等负根,那么实数m应满足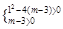 ,解得
,解得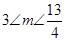 8分
8分设两负根为
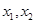 ,则
,则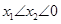 ,可只当
,可只当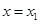 时有极小值
时有极小值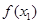 ,由于对称轴为
,由于对称轴为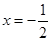 ,
,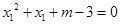 ,
,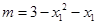
∴
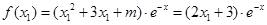 ,
,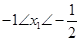 ,
, ∵
∵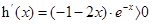
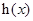 在
在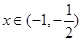 上单调递增
上单调递增∴
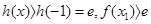
(I)可求出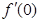 即在点(0,f(0))处切线的斜率,然后写出点斜式方程,再化成一般式即可.
即在点(0,f(0))处切线的斜率,然后写出点斜式方程,再化成一般式即可.
(II)解决本小题的关键是把题目条件若函数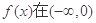 上有两个极值点转化为
上有两个极值点转化为
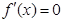 有两个不等的负根,从而借助韦达定理及差别式即可求解.
有两个不等的负根,从而借助韦达定理及差别式即可求解.
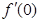 即在点(0,f(0))处切线的斜率,然后写出点斜式方程,再化成一般式即可.
即在点(0,f(0))处切线的斜率,然后写出点斜式方程,再化成一般式即可.(II)解决本小题的关键是把题目条件若函数
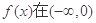 上有两个极值点转化为
上有两个极值点转化为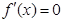 有两个不等的负根,从而借助韦达定理及差别式即可求解.
有两个不等的负根,从而借助韦达定理及差别式即可求解.
练习册系列答案
相关题目
 (a≠0)
(a≠0) ,
, 
 时, 若
时, 若 有
有 个零点, 求
个零点, 求 的取值范围;
的取值范围; , 当
, 当 时恒有
时恒有 , 求
, 求 的最大值, 并求此时
的最大值, 并求此时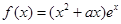 ,其中
,其中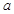 为正实数,
为正实数,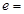 2.7182……
2.7182……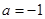 时,求
时,求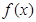 在点
在点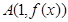 处的切线方程。
处的切线方程。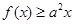 恒成立。
恒成立。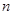 ,设曲线
,设曲线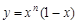 在
在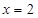 处的切线与
处的切线与 轴交点的纵坐标为
轴交点的纵坐标为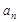 ,
,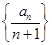 的前
的前 在点
在点 处的切线方程是 。
处的切线方程是 。 ,点P的坐标为 ( )
,点P的坐标为 ( )



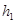 ,
,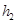 ,
,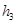 ,
,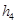 ,则它们的大小关系正确的是( )
,则它们的大小关系正确的是( )
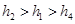
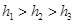
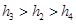
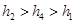
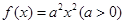 ,
, 。
。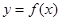 图象上的点到直线
图象上的点到直线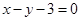 距离的最小值是
距离的最小值是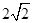 ,求
,求 的值。
的值。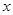 的不等式
的不等式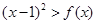 的解集中的整数恰好有3个,求实数
的解集中的整数恰好有3个,求实数