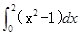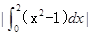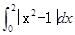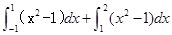题目内容
(16分)设函数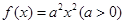 ,
, 。
。
⑴若函数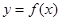 图象上的点到直线
图象上的点到直线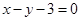 距离的最小值是
距离的最小值是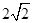 ,求
,求 的值。
的值。
⑵关于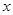 的不等式
的不等式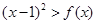 的解集中的整数恰好有3个,求实数
的解集中的整数恰好有3个,求实数 的取值范围。
的取值范围。
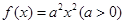 ,
, 。
。⑴若函数
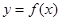 图象上的点到直线
图象上的点到直线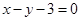 距离的最小值是
距离的最小值是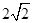 ,求
,求 的值。
的值。⑵关于
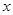 的不等式
的不等式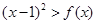 的解集中的整数恰好有3个,求实数
的解集中的整数恰好有3个,求实数 的取值范围。
的取值范围。⑴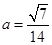 .⑵
.⑵ .
.
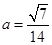 .⑵
.⑵ .
.本试题主要是考查了导数在研究函数与不等式以及点到直线的距离的综合运用。
(1)因为函数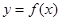 图象上的点到直线
图象上的点到直线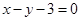 距离的最小值是
距离的最小值是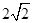 ,则因为
,则因为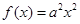 ,所以
,所以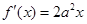 ,令
,令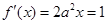 ,解得
,解得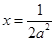 ,此时
,此时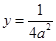 ,则点
,则点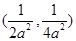 到直线
到直线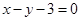 的距离最小可得结论。
的距离最小可得结论。
(2)由于关于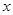 的不等式
的不等式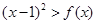 的解集中的整数恰好有3个,等价于
的解集中的整数恰好有3个,等价于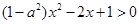 恰好有三个整数解,等价转化思想得到结论。
恰好有三个整数解,等价转化思想得到结论。
⑴因为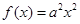 ,所以
,所以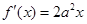 ,令
,令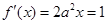 ,解得
,解得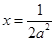 ,此时
,此时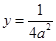 ,则点
,则点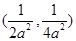 到直线
到直线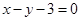 的距离最小,即
的距离最小,即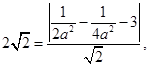 解得
解得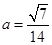 .
.
⑵不等式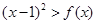 的解集中的整数解恰好有3个,等价于
的解集中的整数解恰好有3个,等价于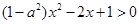 恰好有三个整数解,故
恰好有三个整数解,故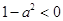 ,即
,即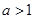 ,
,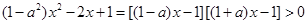 ,所以
,所以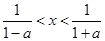 ,又因为
,又因为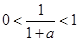 ,所以
,所以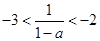 ,解得
,解得 .
.
(1)因为函数
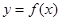 图象上的点到直线
图象上的点到直线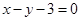 距离的最小值是
距离的最小值是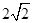 ,则因为
,则因为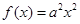 ,所以
,所以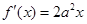 ,令
,令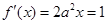 ,解得
,解得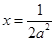 ,此时
,此时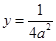 ,则点
,则点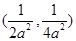 到直线
到直线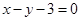 的距离最小可得结论。
的距离最小可得结论。(2)由于关于
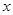 的不等式
的不等式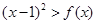 的解集中的整数恰好有3个,等价于
的解集中的整数恰好有3个,等价于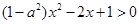 恰好有三个整数解,等价转化思想得到结论。
恰好有三个整数解,等价转化思想得到结论。⑴因为
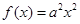 ,所以
,所以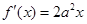 ,令
,令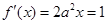 ,解得
,解得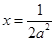 ,此时
,此时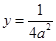 ,则点
,则点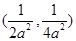 到直线
到直线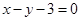 的距离最小,即
的距离最小,即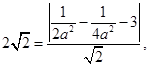 解得
解得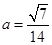 .
.⑵不等式
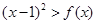 的解集中的整数解恰好有3个,等价于
的解集中的整数解恰好有3个,等价于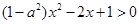 恰好有三个整数解,故
恰好有三个整数解,故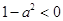 ,即
,即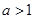 ,
,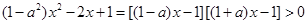 ,所以
,所以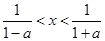 ,又因为
,又因为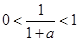 ,所以
,所以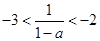 ,解得
,解得 .
.
练习册系列答案
相关题目
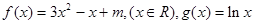
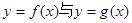 有公共切线时,求函数
有公共切线时,求函数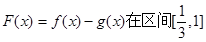 上的最值
上的最值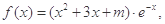 (其中
(其中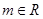 ,
,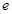 是自然对数的底数)
是自然对数的底数)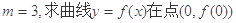 处的切线方程;
处的切线方程;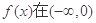 上有两个极值点.
上有两个极值点.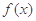 的极小值大于e.
的极小值大于e.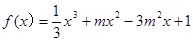
 .
.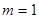 ,求曲线
,求曲线 在点
在点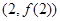 处的切线方程;
处的切线方程;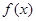 在区间
在区间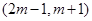 上单调递增,求实数
上单调递增,求实数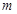 的取值范围.
的取值范围.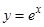 在点
在点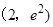 处的切线与两坐标轴所围成的三角形面积为( )
处的切线与两坐标轴所围成的三角形面积为( ) 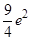
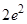
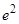
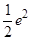
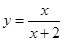 在点
在点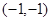 处的切线方程是
处的切线方程是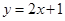
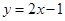
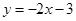
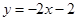
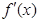 是
是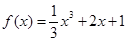 的导函数,则
的导函数,则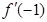 的值是 ____ .
的值是 ____ .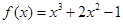 ,则
,则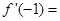 ( )
( )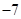
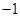
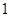
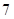
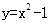 ,直线
,直线 和
和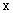 轴围城的封闭图形(阴影)的面积为( )
轴围城的封闭图形(阴影)的面积为( )