题目内容
2．已知函数f（x）=log2x，若f（a）+f（b）=2，则a+b的最小值是4．分析 利用对数的运算性质可得ab=4，再利用基本不等式的性质可得ab$≤（\frac{a+b}{2}）^{2}$，即可得出．
解答 解：∵函数f（x）=log2x，f（a）+f（b）=2，
∴log2a+log2b=2，
化为ab=4，
∴4=ab$≤（\frac{a+b}{2}）^{2}$，
解得a+b≥4，当且仅当a=b=2时取等号．
则a+b的最小值是4．
故答案为：4．
点评 本题考查了对数的运算性质、基本不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
18．已知F1（-c，0），F2（c，0）为椭圆$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点，若椭圆上存在点P满足$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=2c2，则此椭圆离心率的取值范围是（ ）
| A． | [$\frac{1}{2}$，$\frac{\sqrt{3}}{3}$] | B． | （0，$\frac{\sqrt{2}}{2}$] | C． | [$\frac{\sqrt{3}}{3}$，1） | D． | [$\frac{\sqrt{2}}{3}$，$\frac{\sqrt{3}}{3}$] |
13．
设f（x）是一个三次函数，f′（x）为其导函数，如图是函数y=x•f′（x）的图象的一部分，则函数f（x）的极大值是（ ）
设f（x）是一个三次函数，f′（x）为其导函数，如图是函数y=x•f′（x）的图象的一部分，则函数f（x）的极大值是（ ）| A． | f（-1） | B． | f（-2） | C． | f（1） | D． | f（2） |
17．若x，y∈R且满足x+3y=2，则3x+27y+1的最小值是（ ）
| A． | 3$\root{3}{9}$ | B． | 1+2$\sqrt{2}$ | C． | 7 | D． | 6 |
7．已知在△ABC中，∠A、∠B、∠C所对的边是a、b、c，$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$且$\overrightarrow{GA}$•$\overrightarrow{GB}$=0，若（tanA+tanB）•tanC=mtanAtanB，则m的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
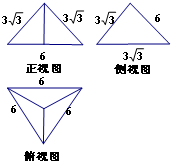正四面体（即各条棱长均相等的三棱锥）的棱长为6，某学生画出该正四面体的三视图如下，其中有一个视图是错误的，则该视图修改正确后对应图形的面积为6$\sqrt{6}$．该正四面体的体积为18$\sqrt{2}$．
12．若复数z满足（3-4i）z=|4+3i|，则z的虚部为（ ）
| A． | $\frac{4}{5}$ | B． | -$\frac{4}{5}$i | C． | $\frac{4}{5}$i | D． | 4 |